09.4. Обобщения второго замечательного предела
Обобщения второго замечательного предела
Докажем, что
Где x – Действительное число, отличное от нуля.
Рассмотрим два случая.
1. 
то есть х принимает положительные значения.
Очевидно, что всякое положительное действительное число x может быть заключено между двумя последовательно стоящими натуральными числами:
Тогда
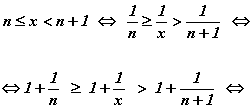
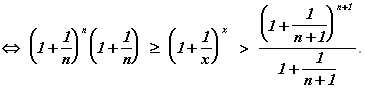
Чтобы применить теорему о пределе промежуточной функции, рассмотрим пределы:
Где 
M = n + 1.
Следовательно, функция 
при 
имеет тот же предел, равный e.
2. Покажем, что и при 
.
Сделаем замену x на –y. Тогда при 
:
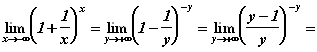
Где 
.
Этим завершается доказательство приведенного выше утверждения.
3. Представим второй замечательный предел в несколько другой форме записи:
Где 
.
Покажем, как второй замечательный предел используется для раскрытия неопределенности вида 
.
Пусть
Покажем, что
(9. 34)
Действительно:
.
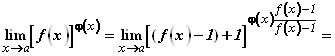
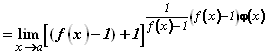Рассмотрим отдельно
Где 
.
Поэтому
Что и требовалось доказать.
Довольно часто второй замечательный предел используется для упрощения вычислений.
Рассмотрим появление такой возможности на конкретной задаче.
Предприятие, осваивая новую технологию, увеличивает ежемесячно выпуск изделий на a% от достигнутого уровня. Сколько потребуется времени, чтобы увеличить первоначальный месячный объем производства более, чем в l раз?
Пусть в первый месяц объем производства составлял А единиц продукции, тогда во второй месяц он будет 
, в третий 
и т. д. Таким образом, требуется найти номер n числовой последовательности
. . . ;
При котором
Или
Примем для определенности: 
и 
. Решая неравенство
Или
,
Находим: 
. Это означает, что потребуется свыше трех лет, чтобы увеличить объем производства более, чем в два раза.
Величину
Можно представить приближенно иначе, воспользовавшись вторым замечательным пределом:
|
При каких n расхождение между величинами |
не превысит 2%, если a=2%?Здесь мы приняли
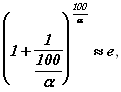
Полагая, что величина 
достаточно большая. Это становится возможным благодаря использованию второго замечательного предела.
| < Предыдущая | Следующая > |
|---|
