09.3. Второй замечательный предел

Второй замечательный предел

Рассмотрим числовую последовательность

.

Может показаться, что она представляет собой созданное лишь самими математиками некоторое искусственное построение. А между тем, трансцендентное число являющееся ее пределом, имеет не меньшее значение в описании окружающего нас мира, чем число . Обозначение буквой это число получило в честь Эйлера в знак признания выдающихся математических достижений этого ученого. Трудно даже представить, что, например, и закон изменения атмосферного давления

(где – атмосферное давление на высоте h над Землей, – атмосферное давление у поверхности Земли, – плотность воздуха на поверхности Земли, g – ускорение свободного падения), и зависимость от времени t толщины пленки y, возникающей при окислении алюминия, цинка или хрома, задаваемая формулой

(где k – постоянная, а ),

И оценка численности A популяции животных за длительный промежуток в t лет

(где – исходная численность животных, а – процент их прироста за один год), Включают в себя одну и ту же константу E. В дальнейшем мы покажем, что есть такая удивительная показательная функция , называемая экспонентой, скорость изменения которой в каждой точке области определения совпадает со значением самой функции в этой точке.

Второй замечательный предел:

(9.32)

Раскрывает неопределенность , так как а

Приемы вычисления этого предела богаты и разнообразны. Мы ограничимся лишь доказательством самого факта его существования. Для этого воспользуемся неравенством Бернулли:

Которое мы докажем методом полной математической индукции. Суть метода состоит в том, что некоторое утверждение, зависящее от натурального параметра n, проверяется при значении n = n0. Далее предлагается его справедливость при k > n0 и доказывается, что при k + 1 оно также верно. Если это удается сделать, то утверждение справедливо при любом n, начиная с n0.

Применительно к неравенству Бернулли при n1 = 1 получим

То есть оно верно. Предположим, что неравенство справедливо для натурального числа k:

Тогда при n = k + 1 будем иметь:

То есть

Справедливость неравенства при n = k + 1 доказана. Следовательно, оно справедливо при любом N.

Приступим к доказательству существования второго замечательного предела. Введем вспомогательную числовую последовательность

; .

Если удастся доказать, что существует, то так как это будет означать, что также существует, причем . Воспользуемся теоремой Вейерштрасса: покажем, что числовая последовательность монотонно убывает и ограничена снизу. Тогда она и будет иметь предел. Ограниченность снизу числовой последовательности очевидна: все ее члены больше нуля. Для доказательства монотонного убывания покажем, что

(9. 33)

Действительно:

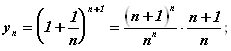
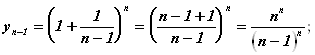
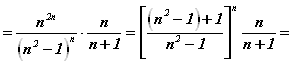
Применим к выражению Неравенство Бернулли, полагая, что :

Поэтому

Таким образом, неравенство (4.33) справедливо. Числовая последовательность отвечает требованиям теоремы Вейерштрасса, значит, она сходится, из чего следует существование и второго замечательного предела (4.32).

< Предыдущая		Следующая >