09.1. Вычисление пределов

Можно ли неарифметическую операцию – Предельный переход – Уподобить арифметической, имеющей место на множестве действительных чисел? Будет ли, например, предел суммы двух функций равен сумме пределов? Иными словами, можно ли, вычисляя , перейти к вычислению пределов и ? Возможно ли заменить вычисление суммы двух пределов вычислением одного: ? Ответы на данные вопросы не очевидны. Означает ли, например, что если

То

Чтобы ответить на эти и другие вопросы, связанные с вычислением пределов, докажем следующие теоремы.

ТЕОРЕМА 1. Для того, чтобы существовал

Необходимо и достаточно, чтобы в окрестности предельной точки A было выполнимо равенство

Где – бесконечно малая функция в окрестности этой предельной точки, то есть

ДОКАЗАТЕЛЬСТВО.

Данное утверждение включает в себя прямую и обратную теоремы. Докажем их.

НЕОБХОДИМОСТЬ. Пусть

.

Покажем, что в окрестности предельной точки a

Где

Действительно, так как

То отсюда следует, что

Еcть бесконечно малая функция в окрестности предельной точки a, или

,

Что и требовалось доказать.

ДОСТАТОЧНОСТЬ. Пусть в окрестности предельной точки a функция связана с числом A соотношением

Где – бесконечно малая функция в окрестности этой предельной точки. Тогда число A есть предел при x, стремящемся к a.

Действительно, так как

Является бесконечно малой функцией в окрестности предельной точки a, то

Что и требовалось доказать.

Эта теорема имеет ключевое значение в обосновании правил вычисления пределов, которые мы сформулируем в виде теоремы.

ТЕОРЕМА 2. Если существуют пределы

, ,

То существуют и пределы

, ,
, ,

Причем справедливы соотношения :

,

, (9. 31)

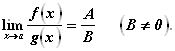
ДОКАЗАТЕЛЬСТВО.

Теорема 1 позволяет в окрестности предельной точки a представить функции и следующим образом:

Где и – бесконечно малые функции в окрестности этой точки. Поэтому

Где

Где

Теперь становится очевидным ответ на вопрос, можно ли все-таки считать

Из свойств бесконечно малых функций следует, что функция , как и функции и , являются бесконечно малыми в окрестности предельной точки a, что и доказывает теорему.

Докажите, что постоянный множитель можно выносить за знак предела.

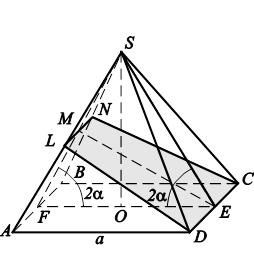
Рис. 9.18. Нахождение площади сечения пирамиды.

 

Вернемся теперь к задаче, поставленной в начале данной главы. Если помните, это была задача о вычислении площади сечения правильной четырехугольной пирамиды в предельном случае, когда A®0 (см. рис. 9.1). Выполним дополнительные построения, позволяющие найти линейные углы для соответствующих двугранных (рис. 9.18). Найдем площадь искомого сечения, являющегося трапецией.

.

Из треугольника FME по теореме синусов получим

Так как ~ , то

В треугольнике SFO находим:

Из треугольника MES получаем:

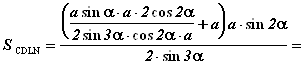
Рассмотрим предел функции при A, стремящемся к нулю:

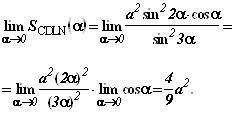
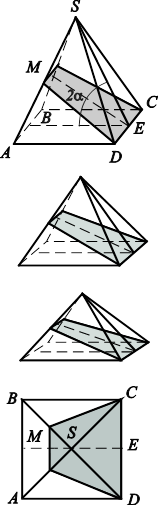
Рис. 9.19. Предельное положение сечения пирамиды при .

Здесь мы воспользовались эквивалентностью функций:

при .

Оказалось, что предельное значение площади в два с лишним раза меньше площади квадрата в основании пирамиды (рис. 9.19). Этот результат трудно было бы предсказать при помощи интуиции.

< Предыдущая		Следующая >