08.6. Бесконечно малые функции и их свойства
Бесконечно малые функции и их свойства
|
Весь мир есть не что иное, как бесконечное пространство, наполненное бесконечно малыми бесцветными и беззвучно движущимися частицами материи. Л. Н. Толстой |
Бесконечно малые функции являются частным случаем функций, имеющих предел.
Функция ![]() называется БЕСКОНЕЧНО МАЛОЙ в окрестности некоторой предельной точки a, если ее предел при x, стремящемся к a, равен нулю.
называется БЕСКОНЕЧНО МАЛОЙ в окрестности некоторой предельной точки a, если ее предел при x, стремящемся к a, равен нулю.
Отсюда следует:
![]()
То есть для X ¹ A И достаточно близких к А значения функции по абсолютной величине становятся меньше любого положительного числа E.
В данном случае предельная точка конечна, однако она может быть и бесконечной. Говорить о бесконечно малой функции можно только в окрестности какой-либо точки. Одна и та же функция может быть бесконечно малой или же бесконечно большой, но в разных предельных точках.
Например, функция
![]()
Как легко показать, бесконечно мала при x, стремящемся к ![]() . Но она будет и бесконечно большой при x, стремящемся к 1, а при x, стремящемся, допустим, к –7, она может быть ни той, ни другой.
. Но она будет и бесконечно большой при x, стремящемся к 1, а при x, стремящемся, допустим, к –7, она может быть ни той, ни другой.
Изучим подробнее свойства бесконечно малых функций. Это позволит нам не только найти способ сравнения между собой таких функциональных зависимостей, но и обосновать правила вычисления пределов. Рассмотрим случай, когда предельная точка конечна. Но надо сказать, что приведенные ниже теоремы справедливы и при ![]() .
.
ТЕОРЕМА 1. Если в окрестности предельной точки a функция ![]() бесконечно мала, то функция
бесконечно мала, то функция ![]() является бесконечно большой в окрестности этой предельной точки.
является бесконечно большой в окрестности этой предельной точки.
ДОКАЗАТЕЛЬСТВО.
По условию теоремы,
![]()
Это означает, что в проколотой D–Окрестности предельной точки a справедливо неравенство
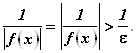
Так как E – любое положительное число, то положительное число N = 1 / E может быть сделано сколь угодно большим. Тогда
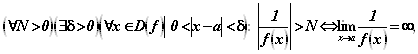
Что и требовалось доказать.
ТЕОРЕМА 2. Если в окрестности предельной точки a функция ![]() бесконечно большая, то функция
бесконечно большая, то функция ![]() является бесконечно малой в окрестности этой предельной точки.
является бесконечно малой в окрестности этой предельной точки.
|
Доказать самостоятельно. |
Доказательство этой теоремы аналогично доказательству предыдущей.
ТЕОРЕМА 3. Сумма конечного числа бесконечно малых функций в окрестности предельной точки a есть функция бесконечно малая в этой же окрестности.
ДОКАЗАТЕЛЬСТВО.
Не умаляя общности рассуждений, ограничимся рассмотрением двух функций: f(x) и g(x), каждая из которых бесконечно мала при ![]() :
:
![]()
![]()
В наименьшей из двух окрестностей ![]() и
и ![]() предельной точки a, которую мы обозначим через D, будут справедливы оба неравенства
предельной точки a, которую мы обозначим через D, будут справедливы оба неравенства
![]() и
и ![]()
Поэтому в D–Окрестности предельной точки A будет иметь место соотношение
![]()
Так как E – любое положительное число, то и положительная величина ![]() также может быть сделана сколь угодно малой. Поэтому
также может быть сделана сколь угодно малой. Поэтому
![]()
![]() ,
,
Что и требовалось доказать.
Важным условием данной теоремы является конечность числа рассматриваемых бесконечно малых функций. Оказывается, что если число слагаемых в сумме бесконечно малых функций бесконечно велико, то их сумма вовсе может и не быть бесконечно малой величиной. Эта особенность явится в последующем предметом глубокого изучения при рассмотрении определенного интеграла.
ТЕОРЕМА 4. Если в окрестности предельной точки a функция ![]() бесконечно мала, а
бесконечно мала, а ![]() ограничена, то их произведение – бесконечно малая функция в окрестности этой предельной точки.
ограничена, то их произведение – бесконечно малая функция в окрестности этой предельной точки.
ДОКАЗАТЕЛЬСТВО.
Пусть ![]() Бесконечно мала, а
Бесконечно мала, а ![]() Ограничена в окрестности предельной точки a. Тогда
Ограничена в окрестности предельной точки a. Тогда
![]()
“![]() ограничена”
ограничена” ![]()
![]() .
.
Наименьшую из двух окрестностей ![]() и
и ![]() обозначим через D. Тогда в этой окрестности будет справедливо соотношение
обозначим через D. Тогда в этой окрестности будет справедливо соотношение
![]()
Так как E – любое положительное число, то положительная величина ![]() тоже может быть любой
тоже может быть любой
![]()
Что и требовалось доказать.
СЛЕДСТВИЕ. Произведение двух бесконечно малых функций есть функция бесконечно малая.
Этот факт очевиден, так как функция, имеющая конечный предел, как доказано ранее, ограничена.
В математическом анализе не только выделяются бесконечно малые функции, но и сравниваются степени их малости. Это, в частности, позволяет заменять одни бесконечно малые функции другими, упрощая тем самым изучение функциональных зависимостей. Следует иметь в виду, что каждый раз при сравнении бесконечно малых речь идет только о некоторой окрестности предельной точки.
Будем называть функцию ![]() БЕСКОНЕЧНО МАЛОЙ БОЛЕЕ ВЫСОКОГО ПОРЯДКА МАЛОСТИ, чем
БЕСКОНЕЧНО МАЛОЙ БОЛЕЕ ВЫСОКОГО ПОРЯДКА МАЛОСТИ, чем ![]() в окрестности предельной точки a, если
в окрестности предельной точки a, если
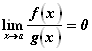 .
.
Принято обозначение:
![]()
Будем называть бесконечно малые функции ![]() и
и ![]() в окрестности предельной точки a БЕСКОНЕЧНО МАЛЫМИ ФУНКЦИЯМИ ОДИНАКОВОГО ПОРЯДКА МАЛОСТИ, если
в окрестности предельной точки a БЕСКОНЕЧНО МАЛЫМИ ФУНКЦИЯМИ ОДИНАКОВОГО ПОРЯДКА МАЛОСТИ, если
|
Доказать, что если |

![]()
В частном случае, при ![]() , бесконечно малые функции, имеющие одинаковый порядок малости, называются ЭКВИВАЛЕНТНЫМИ и обозначаются следующим образом:
, бесконечно малые функции, имеющие одинаковый порядок малости, называются ЭКВИВАЛЕНТНЫМИ и обозначаются следующим образом:
![]()
Первый замечательный предел является подтверждением эквивалентности функций
Y =![]() и Y = X при
и Y = X при![]()
![]() .
.
Укажем еще некоторые часто встречающиеся при решении задач эквивалентные функции (доказательство их эквивалентности может быть осуществлено различными методами математического анализа, которые в дальнейшем нам предстоит рассмотреть).
При ![]()
![]() ~
~![]() ~
~![]() ~
~![]()
![]()
![]()
![]()
![]()
| < Предыдущая | Следующая > |
|---|