08.2. Первый замечательный предел
Первый замечательный предел
В математике получено не так уж много результатов, название которых сопровождается такой восторженной оценкой. Однако строгое построение математической теории иногда все-таки допускает эмоциональный всплеск по поводу достигнутого результата. Чем же замечателен предел
![]() ,
,
Который нам предстоит изучить?
Поведение функции
![]() (9. 25)
(9. 25)
Легко угадывается для достаточно больших по модулю значений x. Однако при малых по абсолютной величине значениях аргумента предвидеть поведение этой функции трудно: и числитель ![]() , и знаменатель x стремятся к 0 при
, и знаменатель x стремятся к 0 при ![]() . Даже самые современные ЭВМ, достигнув своего порога возможностей, уже не смогут осуществить вычисление функции (9.25). Мы можем лишь предположить, что
. Даже самые современные ЭВМ, достигнув своего порога возможностей, уже не смогут осуществить вычисление функции (9.25). Мы можем лишь предположить, что ![]() близок к 1 или, может, даже равен 1. Не исключено, однако, что этим пределом могло бы быть, к примеру, число 0,9999999993 или же 1,000000002. Непосредственные расчеты просто не позволяют в точности это установить, какими бы мощными вычислительными средствами мы ни располагали. Алгебраическая операция
близок к 1 или, может, даже равен 1. Не исключено, однако, что этим пределом могло бы быть, к примеру, число 0,9999999993 или же 1,000000002. Непосредственные расчеты просто не позволяют в точности это установить, какими бы мощными вычислительными средствами мы ни располагали. Алгебраическая операция ![]() недопустима. Но рассмотреть предельный переход в такой ситуации возможно. Теория пределов характеризует этот случай как раскрытие неопределенности, обозначаемой
недопустима. Но рассмотреть предельный переход в такой ситуации возможно. Теория пределов характеризует этот случай как раскрытие неопределенности, обозначаемой
![]() .
.
Существуют еще и другие неопределенности, которые мы изучим в дальнейшем.
Докажем, что
![]() ,
,
Раскрыв при этом указанную неопределенность.
|
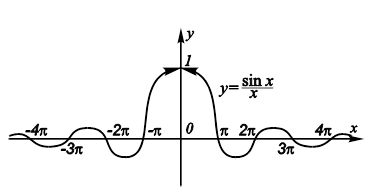
Рис. 9.10. График функции |
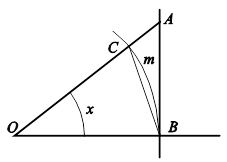
Функция ![]() (рис. 9.10) четна, поэтому доказательство существования предела достаточно провести только для положительных значений x. Рассмотрим дугу BmC единичной окружности (рис. 9.11), соответствующую углу x радиан. Построим
(рис. 9.10) четна, поэтому доказательство существования предела достаточно провести только для положительных значений x. Рассмотрим дугу BmC единичной окружности (рис. 9.11), соответствующую углу x радиан. Построим ![]() и хорду BC. Площадь сектора OBmC больше площади треугольника OBC, но меньше площади треугольника OBA. Используя этот факт, получим:
и хорду BC. Площадь сектора OBmC больше площади треугольника OBC, но меньше площади треугольника OBA. Используя этот факт, получим:
![]()
![]()
![]()
![]()
![]() (9. 26)
(9. 26)
![]()
|
Рис. 9.11. Сравнение площадей вспомогательных фигур, используемое для доказательства первого |
![]()
Функции ![]() и
и ![]() , входящие в последнее двойное неравенство, являются четными, поэтому оно справедливо для любого
, входящие в последнее двойное неравенство, являются четными, поэтому оно справедливо для любого ![]() . Следовательно, при
. Следовательно, при ![]() предел отношения
предел отношения ![]() заключен между 1 и
заключен между 1 и ![]() .
.
Докажем, что
![]() (9. 27)
(9. 27)
Рассмотрим неравенство
![]()
И найдем соответствующую проколотую D–Окрестность нуля:
![]() (9. 28)
(9. 28)
Согласно неравенствам (9.26),
![]()
Поэтому
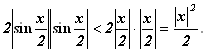
Это означает, что значения x, при которых справедливо неравенство
![]() , (9. 29)
, (9. 29)
Удовлетворяют и неравенствам (9.28).
Еще раз отметим, что нас интересует не точная оценка всех значений x, обеспечивающих выполнение неравенства ![]() , а всего лишь факт существования проколотой D–Окрестности, охватывающей, возможно, и не все значения x, при которых это неравенство справедливо. Поэтому, решая более простое неравенство (9.29), получаем
, а всего лишь факт существования проколотой D–Окрестности, охватывающей, возможно, и не все значения x, при которых это неравенство справедливо. Поэтому, решая более простое неравенство (9.29), получаем
![]()
Значит, по любому положительному числу ![]() можно выбрать D–Окрестность, полагая, что
можно выбрать D–Окрестность, полагая, что
|
Доказан для |
![]()
Итак, предел (9.27) существует. Таким образом, по теореме о пределе промежуточной функции, ![]() тоже равен 1, что и требовалось доказать.
тоже равен 1, что и требовалось доказать.
| < Предыдущая | Следующая > |
|---|