08.1. Свойства пределов

Свойства пределов

Что могут дать знания о пределе функции в какой-либо точке для изучения свойств функциональной зависимости? Может ли функция иметь несколько пределов в одной точке? Эти и другие вопросы возникают сразу после введения данного понятия. Неужели каждый раз отыскание предела должно быть основано на гипотезе о том, что какое-то число А является пределом функции; ведь найти это число и доказать соответствующее предположение, порой, очень трудно. Знания свойств пределов, которые нам предстоит изучить, позволяют не только по-новому взглянуть на ставшие уже привычными понятия математики. Они являются основой для получения практических методов вычисления пределов. За каждой из доказываемых теорем стоят богатейшие физические аналогии и интерпретации из самых различных областей математики. Эти теоремы явились итогом длительных размышлений нескольких поколений математиков о смысле понятия предела. Именно эти теоремы побудили философов задуматься о том, что предельный переход наполняет новым смыслом такие философские категории, как движение и развитие, вносит в них диалектику конечного и бесконечного.

Рассмотрим теоремы о пределах.

ТЕОРЕМА 1. Если функция имеет предел при x, стремящемся к a, то он единственен.

ДОКАЗАТЕЛЬСТВО.

Проведем рассуждения методом от противного. Пусть функция при имеет два предела . Это означает:

(9. 19)

(9. 20)

Окрестности и могут не совпадать между собой, но на меньшей из них будут справедливы оба неравенства:

Так как рассуждения справедливы для любого E, то для

Имеем:

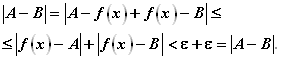
Как в данной теореме используется тавтология, отражающая схему доказательства метода “от противного”?

Получили очевидное противоречие:

Которое свидетельствует о том, что допущения (9.19) и (9.20) одновременно невозможны.

ТЕОРЕМА 2. Если функция имеет предел при x, стремящемся к a, равный A, то она ограничена в некоторой окрестности предельной точки.

ДОКАЗАТЕЛЬСТВО.

Существование означает:

Ограниченность в окрестности предельной точки имеет следующий смысл:

“ F (x) – ограничена”

Множеством X для нас является D–Окрестность предельной точки a:

Или

Чтобы доказать существование числа M > 0, обеспечивающего выполнение неравенства

Рассмотрим неравенство

Или

Если , то и . Если , то также, но уже .

Следует учесть, что в самой точке a функция может быть и определена. Поэтому в качестве числа M следует взять наибольшее из чисел:

Или

Что и доказывает теорему.

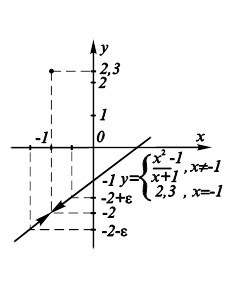
Рассмотрим пример. График функции

Изображен на рис. 9.8.

Рис. 9.8. Ограниченность
рассматриваемой функции
в окрестности предельной
точки.

Выше доказано, что

И получена зависимость D от E:

В качестве числа M можно выбрать наибольшее из чисел:

Если, в частности, , то .

Если же , то .

Существование числа M доказывает ограниченность данной функции в окрестности предельной точки

ТЕОРЕМА 3. Если существует предел функции при x, стремящемся к a, равный A, и , то для достаточно близких к предельной точке a значений аргумента x

ДОКАЗАТЕЛЬСТВО.

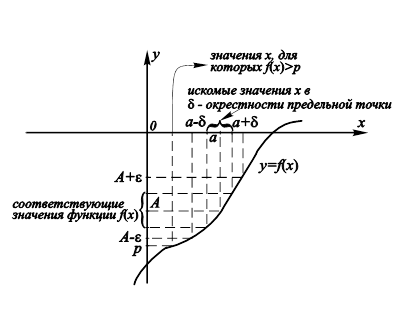
Смысл данной теоремы состоит в том, что если предел A превосходит какое-либо число p, то, приблизившись значениями аргумента достаточно близко к предельной точке a, можно добиться преодоления соответствующего “порога” и самими значениями функции , которые тоже будут больше p. Действительно (рис. 9.9),

Рис. 9.9. Отыскание окрестности предельной точки, обеспечивающей выполнение неравенства .

(9. 21)

Для нас представляет интерес лишь случай

E < A – p. (9. 22)

При E, таких что

Значения x из соответствующей D–Окрестности могут давать значения как большие, так и меньшие p.

Из неравенства

Следует двойное неравенство

Объединяя одно из этих двух неравенств,

С неравенством (9.22), получим систему

Складывая почленно оба неравенства, будем иметь:

Или

Для x, лежащих в D–Окрестности, что и доказывает теорему.

ТЕОРЕМА 4. Если существует предел функции

При , равный A, и , то для достаточно близких к предельной точке a значений аргумента x

Укажите алгоритм нахождения такой окрестности и проведите вычислительный эксперимент на ЭВМ для отыскания требуемых значений применительно к какой-либо функции и конкретных численных значений и

Можно ли в этом утверждении интервал заменить отрезком ?

Эта теорема доказывается аналогично предыдущей.

Из теорем 3 и 4 следует, что каким бы ни был интервал , содержащий число A, всегда найдется такая окрестность предельной точки a, что значения функции будут “попадать” в этот промежуток.