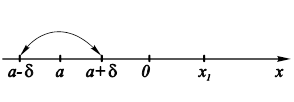07.2. Понятие предела функции
Понятие предела функции
Теория пределов сочетает в себе кажущуюся порой простоту и неисчерпаемую глубину представлений о мире. Нам предстоит познакомиться с уникальными возможностями этой теории в решении прикладных задач. Проникновение основополагающих идей математического анализа в различные области естествознания и техники поражает воображение многих ученых.
Пусть функция ![]() определена на некотором множестве X. Рассмотрим точку a, которая может принадлежать этому множеству или же нет, однако точка a обладает тем свойством, что в любой ее выколотой окрестности
определена на некотором множестве X. Рассмотрим точку a, которая может принадлежать этому множеству или же нет, однако точка a обладает тем свойством, что в любой ее выколотой окрестности ![]() , где D > 0 имеются точки из множества X (рис. 9.3). В таком случае говорят, что точка a является предельной точкой множества X.
, где D > 0 имеются точки из множества X (рис. 9.3). В таком случае говорят, что точка a является предельной точкой множества X.
|
Рис. 9.3. Предельная точка a и ее окрестность. |
Запись x ® a, xÎC означает, что X стремится к предельной точке a. Другими словами, значения x приближаются к a, приобретают значения, все более близкие к a. Это приближение может происходить как слева, так и справа от точки a (рис. 9.3). Какое бы фиксированное значение ![]() мы ни взяли, все равно – по свойству плотности действительных чисел – между числом
мы ни взяли, все равно – по свойству плотности действительных чисел – между числом ![]() и a всегда будет бесконечное множество чисел. Стремление к a следует понимать как абстракцию Потенциальной осуществимости. Поэтому раз и навсегда указать самое близкое к числу a действительное число Невозможно. Вот почему приближение к числу a приобретает характер процесса, причем Бесконечного.
и a всегда будет бесконечное множество чисел. Стремление к a следует понимать как абстракцию Потенциальной осуществимости. Поэтому раз и навсегда указать самое близкое к числу a действительное число Невозможно. Вот почему приближение к числу a приобретает характер процесса, причем Бесконечного.
Как же математически описать этот процесс? Очевидно, надо показать, что значения x будут “стягиваться” к точке a, располагаясь слева и справа от нее или же с одной стороны. Рассмотрим неравенство
![]() (9. 5)
(9. 5)
Где D > 0.
Раскрывая его, получим:
![]()
![]() (9. 6)
(9. 6)
Полученное в ходе преобразований двойное неравенство определяет симметричный относительно точки a интервал ![]() . Причем, уменьшение величины D приводит к уменьшению интервала, который сохранит точку a как центральную точку. Стремление x к a может и не сопровождаться симметричным расположением точек x относительно точки a, уменьшение D не обязательно должно отражать конкретный процесс стремления x к a. Важно другое: при стремлении x к a значения x, не равные a, попадают во все более малый интервал
. Причем, уменьшение величины D приводит к уменьшению интервала, который сохранит точку a как центральную точку. Стремление x к a может и не сопровождаться симметричным расположением точек x относительно точки a, уменьшение D не обязательно должно отражать конкретный процесс стремления x к a. Важно другое: при стремлении x к a значения x, не равные a, попадают во все более малый интервал ![]() с центром в точке a, называемым проколотой D–окрестностью этой точки. Бесконечно близкое приближение к точке a означает наличие в любой ее проколотой D–Окрестности хотя бы одной точки x, отличной от a. Отсюда легко заключить, что в любой проколотой D–Окрестности точки a содержится бесконечно много точек
с центром в точке a, называемым проколотой D–окрестностью этой точки. Бесконечно близкое приближение к точке a означает наличие в любой ее проколотой D–Окрестности хотя бы одной точки x, отличной от a. Отсюда легко заключить, что в любой проколотой D–Окрестности точки a содержится бесконечно много точек ![]() .
.
Предельный переход определяет поведение функции ![]() при х, стремящемся к а. Приближаются ли значения функции
при х, стремящемся к а. Приближаются ли значения функции ![]() ,
, ![]() к некоторому значению A, Когда x Стремится к а? Характер такого приближения можно оценить аналогичным способом, введя в рассмотрение E–Окрестность точки А:
к некоторому значению A, Когда x Стремится к а? Характер такого приближения можно оценить аналогичным способом, введя в рассмотрение E–Окрестность точки А:
![]()
Нельзя считать ![]() , так как в точке а сама функция может быть и не определена.
, так как в точке а сама функция может быть и не определена.
В E–Окрестности точки А будем иметь:
![]() (9. 7)
(9. 7)
Или
![]() . (9. 8)
. (9. 8)
Понятие предела определим следующим образом.
Число А называется ПРЕДЕЛОМ ФУНКЦИИ ![]() при х, стремящемся к а, если для любого
при х, стремящемся к а, если для любого ![]() найдется такое число
найдется такое число![]() , что для всех х, удовлетворяющих условию
, что для всех х, удовлетворяющих условию ![]() , будет выполнятся неравенство
, будет выполнятся неравенство ![]() .
.
Принято обозначение:
![]()
На рис. 9.4 указана одна из возможных проколотых D-окрестностей, соответствующая выбранному ![]() (она обозначена дугой).
(она обозначена дугой).
|
Рис. 9.4. Выбор D-Окрестности по заданной |
Используя логические символы, определение предела можно записать в виде:
![]() (9. 9)
(9. 9)
Высказывание
![]() (9. 10)
(9. 10)
|
Предел – – – где мысль одна горит в небесной чистоте. А. С.Пушкин |
Получено из предиката трех переменных E, D И х, над которым осуществляются кванторные операции.
Этот предикат, исходя из определения предела, можно записать в виде:
![]() (9. 11)
(9. 11)
И представить утверждение (4.10) иначе:
![]() (9. 12)
(9. 12)
Высказывания (4.10), (4.12) в равной мере можно считать определением предела.
Вводя определение предела, мы использовали понятия E-Окрестности предельного значения А функции ![]() и проколотой D-окрестности предельной точки А. С привлечением этих окрестностей оно может быть записано и в виде:
и проколотой D-окрестности предельной точки А. С привлечением этих окрестностей оно может быть записано и в виде:
![]()
Довольно часто данное определение называют определением на языке “E–D”.
Вернемся к функции
У = 2х,
Имеющей D( F ) = R, и покажем, что при ![]() она стремится к 6 (рис. 4.5). Для этого докажем существование предела
она стремится к 6 (рис. 4.5). Для этого докажем существование предела
|
Допустима ли в определении предела замена отдельных знаков строгого неравенства знаками нестрогого неравенства? |
![]()
Функция Y = 2x определена на всей действительной оси, поэтому всякая проколотая D-окрестность лежит в ее области определения.
|
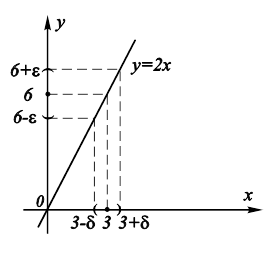
Рис. 9.5. Поведение функции у = 2х в окрестности Предельной точки а = 3. |
Доказательство состоит в том, чтобы показать, как по произвольному положительному числу E найти такое положительное число D, что если только значения х Не будут равны 3 и находиться в промежутке ![]() , то значения функции У=2х Удовлетворят неравенству
, то значения функции У=2х Удовлетворят неравенству ![]() . Иными словами, какой бы ни была Малой окрестность числа 6, размеры которой определяются малостью положительного числа E, всегда найдется достаточно малая окрестность предельной точки а = 3, длина которой задается через положительную величину D, что если х брать из D–Окрестности, то значения функции попадут в E–Окрестность числа 6. Именно поэтому число 6 и будет пределом. Если по любому E удается найти D, то есть указать функцию
. Иными словами, какой бы ни была Малой окрестность числа 6, размеры которой определяются малостью положительного числа E, всегда найдется достаточно малая окрестность предельной точки а = 3, длина которой задается через положительную величину D, что если х брать из D–Окрестности, то значения функции попадут в E–Окрестность числа 6. Именно поэтому число 6 и будет пределом. Если по любому E удается найти D, то есть указать функцию ![]() , то это и означает существование предела
, то это и означает существование предела ![]()
Действительно, из неравенства
![]()
Вытекает
![]()
Отсюда следует, что если значения аргумента х брать из промежутка
![]()
То значения функции у = 2х отклоняются от числа 6 менее чем на ![]() . Например, возьмем E = 0,01. Тогда в качестве D можно взять величину
. Например, возьмем E = 0,01. Тогда в качестве D можно взять величину ![]() или меньше нее (но больше нуля). Пусть это будет D = 0,002. Тогда можно утверждать, что для х из промежутка
или меньше нее (но больше нуля). Пусть это будет D = 0,002. Тогда можно утверждать, что для х из промежутка
2,998 < х < 3,002, ![]()
|
Доказать, что
|
Значения функции у = 2х будут отличаться от числа 6 менее чем на 0,01. Если, к примеру, х = 3,001, то у (3,001)=6,002 и
|6,002-6| = 0,002 < 0,01,
Что и требовалось показать.
Другой пример. Докажем, что
![]()
Функция
![]()
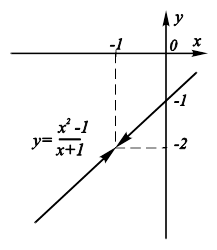
Определена для всех действительных значений X за исключением X = -1. Ее графиком является прямая с “выколотой” точкой М(-1;-2) (рис. 9.6).
|
Рис. 9.6. График функции В окрестности предельной точки |
В предельной точке ![]() данная функция не определена, однако она имеет предел при
данная функция не определена, однако она имеет предел при ![]() , равный –2. Действительно, так как
, равный –2. Действительно, так как ![]() , но
, но ![]() , то
, то ![]() , имеем:
, имеем:
![]()
Это означает, что в качестве величины D может быть взято какое-либо число, меньшее E. Отметим, что достаточно найти Хотя бы одно D, так как в определении предела требуется Существование D, то есть указание хотя бы одного возможного его значения.
Совсем неважно, найдутся ли по величине E и другие значения X, при которых будет выполняться неравенство ![]() . Проколотая D–окрестность предельной точки может и не охватывать все значения x этого неравенства. Важно лишь, чтобы Она существовала. Поэтому при доказательстве существования предела величину D чаще всего Не вычисляют точно, а лишь оценивают. В этом можно убедиться на следующем примере.
. Проколотая D–окрестность предельной точки может и не охватывать все значения x этого неравенства. Важно лишь, чтобы Она существовала. Поэтому при доказательстве существования предела величину D чаще всего Не вычисляют точно, а лишь оценивают. В этом можно убедиться на следующем примере.
Доказать: ![]() .
.
Функция G = X2 определена на R. Имеем:
![]()
Выполним преобразования:
![]()
![]()
![]()
Если неравенство
![]() (9. 13)
(9. 13)
Заменить неравенством
![]() (9. 14)
(9. 14)
То, так как
![]()
Решение неравенства (9.14) будет и решением неравенства (9.13). Но неравенство (9.14) привлекательнее тем, что его легче разрешить относительно величины ![]() , ответственной за длину проколотой D–Окрестности.
, ответственной за длину проколотой D–Окрестности.
Рассматривая (9.14), будем иметь
![]()
Полагаем, что
![]() (9. 15)
(9. 15)
Тогда
![]()
Получаем:
![]() .
.
Но, согласно (4.15), имеем:
![]() (9. 16)
(9. 16)
А потому
![]()
И для x из этой проколотой D–окрестности точки х = 1 будет справедливо и неравенство (9.13). Вместе с тем, неравенству (9.13) будут удовлетворять и другие значения x, которые можно определить путем точного решения. Однако для нас они не важны, поскольку мы интересуемся лишь Существованием проколотой D–окрестности, а для этого достаточна даже грубая оценка ее величины, определяющей допустимые размеры окрестности предельной точки.
Рассмотрим высказывание, отрицающее существование предела:
![]()
![]()
![]()
![]()
Если воспользоваться определением предела в форме (9.12), то будем иметь:
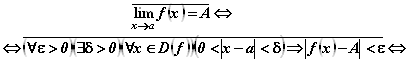
![]()
![]()
В преобразованиях, указанных эквиваленцией, использовалась известная тавтология для высказываний В и С:
![]()
Таким образом, отрицание существования предела может быть записано в двух эквивалентных формах:
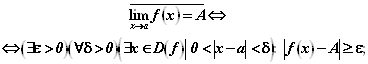 (9. 17)
(9. 17)
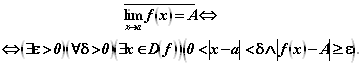 (9.18)
(9.18)
В качестве примера покажем, что
![]()
Для этого необходимо показать справедливость утверждений (9.17) или же (9.18). Рассмотрим для определенности высказывание (9.18):
![]()
Наша цель указать хотя бы одно какое-то положительное число ![]() , при котором в любой проколотой D-Окрестности предельной точки все равно найдутся (существуют) такие x, что модуль разности функции
, при котором в любой проколотой D-Окрестности предельной точки все равно найдутся (существуют) такие x, что модуль разности функции ![]() и этого числа 5 превзойдет E. Действительно, так как расстояние между числом 5 и числом 6 (это число, как доказано, является истинным пределом) равно 1, то в качестве возможного значения E можно взять какую-нибудь величину, меньшую, чем это расстояние (рис. 9.7). Тогда, какой бы ни была проколотая D-Окрестность предельной точки
и этого числа 5 превзойдет E. Действительно, так как расстояние между числом 5 и числом 6 (это число, как доказано, является истинным пределом) равно 1, то в качестве возможного значения E можно взять какую-нибудь величину, меньшую, чем это расстояние (рис. 9.7). Тогда, какой бы ни была проколотая D-Окрестность предельной точки ![]() (то есть для
(то есть для ![]() ), найдется такое
), найдется такое ![]() , что будет выполняться неравенство:
, что будет выполняться неравенство:
![]()
|
Рис. 9.7. Иллюстрация того, что |
Это и означает, что ![]() .
.
| < Предыдущая | Следующая > |
|---|