05.2. Эксцентриситет и директрисы конических сечений

Эксцентриситет и директрисы конических сечений

Изучение кривых второго порядка окажется неполным, если обойти вниманием некоторые их замечательные свойства, используемые в разнообразных приложениях.

Для эллипса, отличного от окружности, а также для гиперболы и параболы обнаруживается универсальное свойство: существует прямая, называемая директрисой (в зависимости от типа кривой их может быть одна или две), для которой отношение расстояния от точек этих кривых до фокуса к расстоянию до отвечающей этому фокусу директрисы есть величина постоянная.

Как известно, в частном случае это свойство справедливо для параболы согласно ее определению. Покажем также справедливость данного свойства для эллипса и гиперболы. Введем предварительно в рассмотрение параметр, характеризующий форму эллипса и гиперболы.

Эксцентриситетом эллипса (гиперболы) будем называть величину

(5.8)

Где с – половина фокусного расстояния эллипса (гиперболы), а – длина большей полуоси эллипса (длина действительной полуоси гиперболы).

Учитывая, что половина фокусного расстояния с и длины полуосей связаны известными соотношениями:

Для эллипса

Для гиперболы

Получим формулы вычисления эксцентриситета этих кривых по параметрам канонических уравнений:

для эллипса (5.9)

для гиперболы (5.10)

Очевидно, что эксцентриситет эллипса меньше единицы, а эксцентриситет гиперболы – больше единицы. Если длины полуосей эллипса близки друг к другу, то его эксцентриситет неограниченно приближается к нулю, а эллипс – к окружности.

Эксцентриситет эллипса характеризует его "сплюснутость": чем он ближе к единице, тем более эллипс "вытянут" вдоль оси абсцисс. На рис. 5.12 показано семейство эллипсов, у которых при постоянной длине большой полуоси а малая полуось меняется.

Рис. 5.12. Влияние величины эксцентриситета
на форму эллипса.

Как по заданным длинам полуосей а и b с помощью циркуля и линейки найти фокусы гиперболы? Изобразите семейство гипербол, у которых мнимая ось постоянна, а действительная полуось а меняется.

Эксцентриситет гиперболы также характеризует "сплюснутость" кривой. Ветви гиперболы расположены между асимптотами

и

Если действительная ось гиперболы совпадает с осью Ох (рис. 5.13), то величина угла между асимптотами будет уменьшаться с уменьшением b при постоянном a, и чем меньше отношение для гиперболы, тем меньше ее эксцентриситет е. На рис. 5.13 показано семейство гипербол, у которых при постоянной длине действительной полуоси a малая полуось b меняется.

0

Рис. 5.13. Влияние величины эксцентриситета
на форму гиперболы.

При определении параболы мы уже столкнулись с описанием этого геометрического места точек с помощью вспомогательной прямой, называемой директрисой. Такая прямая полезна также при изучении свойств эллипса и гиперболы. Более того, сами понятия эллипса и гиперболы могут быть введены через описание их свойств по отношению к директрисам и фокусам.

Будем называть директрисами эллипса, у которого большая полуось расположена вдоль оси Ох, прямые

.

Эти прямые расположены (рис.5.14) вне эллипса (так как ) на одинаковом расстоянии от его центра перпендикулярно оси Ох.

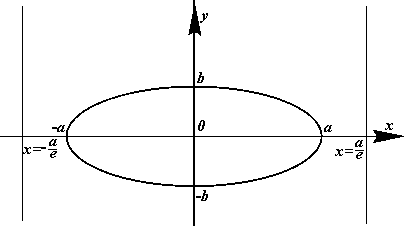
Рис. 5.14. Директрисы эллипса.

Точки эллипса обладают интересным свойством, которое мы сформулируем в виде теоремы.

ТЕОРЕМА 1. Для любой точки эллипса отношение ее расстояния до фокуса к расстоянию до
Соответствующей директрисы равно эксцентриситету.

Доказательство.

Пусть d1 и d2 – расстояния от произвольной точки эллипса до директрис и соответственно (рис. 5.15). Расстояние от этой точки до фокуса будет , а до фокуса =, где, как известно, и  – фокальные радиусы. Теорема утверждает:

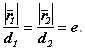
Ранее уже получено: . Учитывая, что , будем иметь:

.

Так как директрисы перпендикулярны главной оси эллипса, то расстояния d1 и d2 находятся как длины отрезков, параллельных оси Ох:

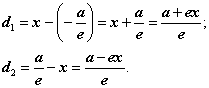
Рис. 5.15. Расстояния от точки эллипса до фокуса
и соответствующей директрисы.

Тогда:

Что и требовалось доказать.

Директрисы для гиперболы вводятся так же, как и для эллипса.

Будем называть директрисами гиперболы, у которой действительная ось расположена на оси Ох, прямые

Эти прямые располагаются (рис. 5.16) между ветвями гиперболы (так как ) на расстоянии от ее центра перпендикулярно оси Ох.

0

Рис. 5.16. Директрисы гиперболы.

Докажем теорему, отражающую свойства директрис гиперболы.

ТЕОРЕМА 2. Для любой точки М(Х,У) гиперболы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равно эксцентриситету е.

Доказательство:

Для доказательства теоремы следует выделить четыре случая:

1. Точка располагается на левой ветви гиперболы, при этом рассматриваются фокус и директриса .

2. Точка находится на левой ветви гиперболы, при этом берутся фокус и директриса .

3. Точка принадлежит правой части гиперболы, при этом рассматриваются фокус и директриса .

4. Точка взята на правой ветви гиперболы, при этом используются фокус и директриса .

Рассуждения во всех этих случаях аналогичны. Выделим один из них, например, четвертый (рис. 5.17).

0

Рис. 5.17. Свойства директрис и фокусов гиперболы.

Для этого случая

Тогда

Такой же результат мы получим в трех других случаях, что и доказывает теорему.

Сформулируем без доказательства теорему, которая позволяет по-новому определить эллипс и гиперболу.

ТЕОРЕМА 3. Геометрическое место точек М, для которых отношение е модуля радиус-вектора к расстоянию d точек М до заданной прямой есть величина постоянная, является эллипсом при и гиперболой при .

Точка F называется фокусом кривой, радиус-вектор  –фокальным радиус–вектором, а упомянутая прямая – директрисой.

Таким образом, есть векторное уравнение эллипса при , либо гиперболы, если , а для оно определяет параболу.

Постройте семейство кривых при фиксированном е и различных d.

Полученный результат означает, что задание параметров e и d однозначно определяет эллипс, гиперболу, параболу.

Эллипс, гипербола и парабола, как уже отмечалось, могут быть получены путем конических сечений. Обоснование этому дает следующая теорема, которую мы приводим также без доказательства.

ТЕОРЕМА 4. Для всякой линии, будь то эллипс (включая окружность), гипербола или парабола, может быть найден такой круговой конус и такая плоскость, что пересечением конуса с этой плоскостью будет являться именно данная кривая.

Связь между этими линиями имеет и алгебраическое обоснование: все они задаются уравнениями второй степени. Можно доказать, что в любой прямоугольной системе координат уравнения таких кривых имеют вид

Где A, B,C, D,E и F – числа, причем

Каков геометрический смысл этого условия?

Справедливо и обратное утверждение: любое алгебраическое уравнение второй степени

Каким будет геометрический образ этого уравнения, когда левая его часть раскладывается на множители?

Определяет эллипс, гиперболу или параболу, если только левая часть уравнения не раскладывается на множители.

Вот почему для эллипса, гиперболы и параболы используется обобщающее название: кривые второго порядка.

< Предыдущая		Следующая >