05.3. Уравнения эллипса, гиперболы и параболы

Уравнения эллипса, гиперболы и параболы
В полярной системе координат

Нам уже известно, что в полярной системе координат окружность с центром в начале отсчета задается уравнением:

,

Где r – радиус окружности, а  – полярный радиус.

Интуитивно легко угадывается расположение начала отсчета, при котором уравнение окружности имеет более простой вид. Эта проблема усложняется при выводе уравнений эллипса, гиперболы и параболы.

Рассмотрим сначала отличный от окружности эллипс и параболу. Проведем рассуждения для параболы. Пусть начало полярной системы координат находится в полюсе F, а полярная ось перпендикулярна директрисе и ориентирована, как указано на рис. 5.18. Возьмем произвольную точку на данной кривой.

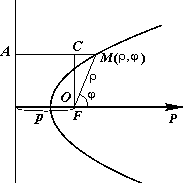
Рис. 5.18. Расположение полярной системы координат при выводе уравнений эллипса и параболы.

Как уже известно, для точек эллипса и параболы и только для них

Где – расстояние от этой точки до фокуса F, а  – расстояние до директрисы, е – эксцентриситет.

Так как

И

Где р – расстояние от фокуса F до директрисы, то

Как параметр р выражается через полуоси эллиптической кривой?

Или

Каким будет уравнение этих кривых, если начало полярной системы координат перенести в точку С, а полярную ось - параллельно самой себе, не меняя ориентации ?

(5.11)

Это есть уравнение эллипса или параболы в полярной системе координат.

Перейдем к выводу уравнения гиперболы в полярной системе координат.

Пусть F – один из фокусов гиперболы (рис.5.19), а р=AC,  – эксцентриситет гиперболы. Располагаем начало отсчета в фокусе F и ориентируем полярную ось, как указано на рис. 5.19.

Рис. 5.19. Расположение полярной системы координат при выводе уравнения гиперболы.

Для правой ветви гиперболы, повторяя предыдущие рассуждения, сразу получим уравнение вида (5.11).

Найдем уравнение левой ветви. Для точек гиперболы будет справедливо соотношение . Пусть  – произвольная точка, лежащая на левой ветви (рис. 5.19). Имеем:

Тогда уравнение левой ветви гиперболы примет вид:

Или

.

Таким образом, полярное уравнение гиперболы имеет вид:

В каких пределах изменяется угол для обеих ветвей?

- для правой ветви;

- для левой ветви.

 

< Предыдущая		Следующая >