04.14. Смешанное произведение векторов

Смешанное произведение векторов

Произведение трех векторов может быть введено разными способами, вытекающими из уже введенных действий: скалярного и векторного произведений векторов, умножения вектора на скаляр. Рассмотрим возможные варианты такого умножения.

Пусть даны три вектора: , И . Если два из них перемножить скалярно и результат умножения – скаляр – умножить на третий вектор, то мы получим вектор, коллинеарный этому третьему вектору. Причем, такое произведение будет зависеть от того, какие два вектора перемножены вначале, то есть не будет выполняться сочетательный закон умножения векторов:

.

Возможны еще и произведения вида , также . Исследуем подробнее векторно-скалярное произведение векторов , связав его с решением прикладных задач. Его будем называть для краткости СМЕШАННЫМ ПРОИЗВЕДЕНИЕМ ВЕКТОРОВ.

Пусть

Известно, что

Где J – угол между векторами и . Эта величина равна площади параллелограмма, построенного на векторах и как на сторонах (рис. 3.36).

Умножая скалярно на , мы получим скаляр

,

Где Y – угол между векторами и .

Рис. 3.36. Геометрическая интерпретация смешанного произведения векторов.

Отсюда становится понятным геометрический смысл смешанного произведения векторов: оно равно По модулю объему параллелепипеда, построенного на векторах , И как на ребрах.

Приведите примеры использования смешанного произведения в физике.

Смешанное произведение обратится в нуль, когда какой-либо из векторов – нулевой или же когда векторы компланарны (то есть лежат в одной плоскости). Очевидно, что и объем параллелепипеда, построенного на таких векторах как на ребрах, обратится в нуль.

Рассмотрим свойства смешанного произведения.

1. – сочетательный закон. Его справедливость вытекает из того, что эти произведения имеют одинаковые модули. Кроме того, тройка векторов , , , будучи правой или же левой в произведении , останется таковой, если ее заменить на тройку , , , что соответствует произведению .

Следовательно, произведения и равны, что дает нам основания упростить запись смешанного произведения векторов. Вот почему для смешанного произведения трех векторов используется обозначение:

2.  – закон круговой переместительности.

Так как знак векторного произведения можно поставить между любой парой рядом стоящих векторов, и это произведение подчиняется антипереместительному закону, то перемена мест рядом стоящих сомножителей в смешанном произведении приводит к изменению его знака,

Круговая перестановка трех сомножителей, как мы видим, не меняет его величины.

3. – сочетательный закон относительно скалярного множителя.

Этот закон непосредственно вытекает из соответствующих законов для скалярного и векторного произведения двух векторов.

Выведем формулы вычисления смешанного произведения в координатной форме. Пусть в системе координат 0xyz заданы три вектора:

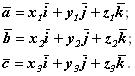
Найдем как произведение :

Раскрывая скобки, получим окончательный результат:

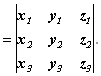
Из этой формулы следует условие компланарности векторов , И в координатной форме:

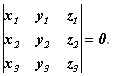
< Предыдущая		Следующая >