04.13. Векторное произведение векторов

Векторное произведение векторов

Так же, как и скалярное произведение, векторное произведение своим появлением обязано необходимости решения физических задач. Рассмотрим одну из таких – задачу о вычислении момента силы.

Принято считать моментом силы , приложенной в точке А относительно точки О, вектор , имеющий модуль, равный произведению модуля силы на кратчайшее расстояние (плечо силы) от этой точки до линий действия силы (рис 3.33). Если вектор связывает точку О с началом вектора , а  – угол между векторами И , то .

Поэтому .

Вектор перпендикулярен плоскости, в которой лежат сила и точка О, и ориентирован в ту сторону, откуда вращение тела вокруг точки О видно как вращение, происходящее против часовой стрелки. Таким образом, двум векторным величинам И Ставится в соответствие тоже векторная величина. Это новый тип соответствия отличен от уже введенного скалярного произведения. Существуют разнообразные физические процессы, в которых соответствие между векторами осуществляется подобным образом. Вот почему в математике вводится еще одно действие умножения векторов – векторное произведение.

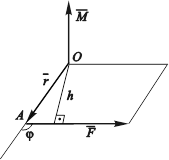
Рис. 3.33. Момент силы относительно точки О.

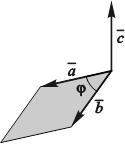
ВЕКТОРНЫМ ПРОИЗВЕДЕНИЕМ вектора на вектор называется вектор , обозначаемый , обладающий следующими свойствами (рис. 3.34):

1. Его модуль равен произведению модулей данных векторов на синус угла между ними.

2. Он перпендикулярен плоскости, в которой располагаются данные векторы.

Рис. 3.34. Векторное произведение векторов.

3. Его ориентация такова, что векторы , и образуют правую координатную тройку (то есть из конца вектора поворот от вектора до совмещения с вектором на кратчайший угол виден как поворот, осуществляемый против часовой стрелки).

По определению имеем:

Справедливо ли утверждение ?

Геометрически это означает, что равняется площади параллелограмма, построенного на векторах и как на сторонах.

Возвращаясь к задаче о вычислении момента силы, можно заключить, что

и .

Очевидно, что векторное произведение обращается в нуль , если векторы коллинеарны или же какой-нибудь из них нулевой.

Рассмотрим алгебраические свойства векторного произведения. Не все они сохраняются в том же виде, что и для скалярного произведения.

1.  – антипереместительный закон.

Объясните физический смысл антипереместительного закона

Действительно, векторы и перпендикулярны одной и той же плоскости, в которой располагаются векторы и , но ориентированы в противоположные стороны, так как, если векторы , , образуют правую тройку, то векторы , , будут образовывать уже левую тройку векторов, что и доказывает данный закон.

2.  – распределительный закон. Приведем его без доказательства.

3.  – сочетательный закон относительно скалярного множителя.

Найти

Действительно, векторы и (рис. 3.35) имеют одинаковые модули. Их ориентация совпадает с ориентацией вектора , если , и противоположны ему при .

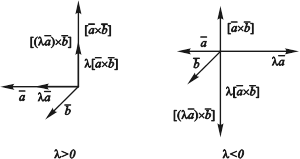
Рис. 3.35. Сочетательный закон для векторного
произведения векторов относительно скалярного
Множителя.

Очевидно, что векторный квадрат вектора равен нулю:

Получим формулы векторного произведения в координатном виде. Пусть даны векторы:

Поэтому

Векторные квадраты координатных ортов равны нулю:

А произведения определяются следующим образом:

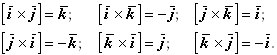
Тогда

Эта запись может быть представлена в компактной форме с помощью определителя третьего порядка.

Определителем третьего порядка, составленного из таблицы девяти элементов

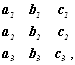
Называется выражение

.

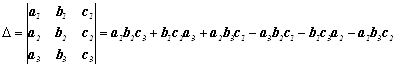Произведения элементов определителя, которые берутся со знаком плюс, символично для запоминания могут быть представлены следующей схемой:

Последние три слагаемых определителя, имеющие знак минус, получаются по другой схеме:

В курсе алгебры при решении систем линейных уравнений рассматриваются определители различных порядков, элементами которого чаще всего являются числа, а потому и определитель есть число.

Легко проверить справедливость формулы:

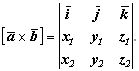
В заключение получим интересную формулу, связывающую скалярное и векторное произведения.

Так как

То очевидно соотношение:

Отсюда можно получить два полезных неравенства:

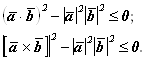
< Предыдущая		Следующая >