04.12. Скалярное произведение векторов
Скалярное произведение векторов
Рассмотрим задачу о вычислении работы. Проблема может показаться простой, если материальная точка M перемещается по прямой, а действие силы ![]() совпадает с направлением движения (рис. 3.32, а).
совпадает с направлением движения (рис. 3.32, а).

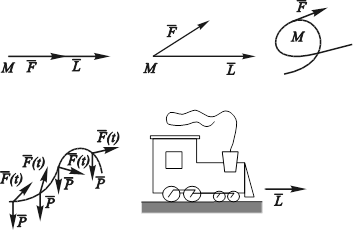
Рис. 3.32. Физические схемы вычисления работы материальной точки.
Однако эта классическая задача физики интересна тем, что ее возможные усложнения служили толчком к развитию фундаментальных математических идей. Какие же трудности следует ожидать при ее решении? Во-первых, направления действия силы и перемещения L могут не совпадать (рис. 3.32, б); во-вторых, путь может и не быть прямолинейным (рис. 3.32, в); в-третьих, сила может быть переменной, изменяясь в зависимости от пути, времени, скорости точки и т. д., да и самих сил, приложенных к одной точке, может быть несколько (рис. 3.32, г); в-четвертых, далеко не всегда тело, представляющее собой систему, в которой преобразуются различные типы энергии, можно рассматривать как материальную точку (рис. 3.32, д). Эта задача проходит через всю историю математики, заставляя удивляться и физиков универсальности математических знаний. Идеи, используемые для вычисления работы, применимы при решении других, казалось бы, совсем не схожих проблем. Математика помогает естествознанию понять единство мира.
Рассмотрим случай, когда прямолинейное перемещение L не совпадает с направлением постоянной силы ![]() , действующей на материальную точку М (см. рис. 3.32, б). Тогда работа А вычисляется по известной формуле:
, действующей на материальную точку М (см. рис. 3.32, б). Тогда работа А вычисляется по известной формуле:
![]()
Где A – угол между направлениями перемещения ![]() и силы
и силы ![]() .
.
Математическая суть этой формулы в том, что двум векторным величинам ![]() и
и ![]() поставлена в соответствие скалярная величина А. Такая связь величин послужила основанием для введения математического действия умножения векторов, по которому результатом выполнения данной операции является скаляр. Введение такого действия тем более необходимо, что к подобным преобразованиям сводятся многие задачи физики и самой математики. Конечно, было бы желательно, чтобы вводимое действие обладало свойствами, аналогичными свойствам умножения скалярных величин, и соответствовало свойствам объектов реального мира.
поставлена в соответствие скалярная величина А. Такая связь величин послужила основанием для введения математического действия умножения векторов, по которому результатом выполнения данной операции является скаляр. Введение такого действия тем более необходимо, что к подобным преобразованиям сводятся многие задачи физики и самой математики. Конечно, было бы желательно, чтобы вводимое действие обладало свойствами, аналогичными свойствам умножения скалярных величин, и соответствовало свойствам объектов реального мира.
Итак, дадим определение новому действию – скалярному произведению векторов.
СКАЛЯРНЫМ произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
|
Справедливо ли утверждение |
Скалярное произведение двух векторов ![]() и
и ![]() будем обозначать следующим образом:
будем обозначать следующим образом: ![]() .
.
По определению, ![]() где J – угол между векторами.
где J – угол между векторами.
Это определение можно переписать иначе:
![]() .
.
Из определения следует, что скалярное произведение равно произведению модуля одного вектора и проекции на него другого вектора.
Скалярное произведение обратится в нуль, если векторы взаимно перпендикулярны или же какой-либо из них нулевой.
Рассмотрим алгебраические свойства скалярного произведения:
1. ![]() – переместительный закон, справедливость которого следует из определения скалярного произведения и свойств действительных чисел.
– переместительный закон, справедливость которого следует из определения скалярного произведения и свойств действительных чисел.
2. ![]() – распределительный закон.
– распределительный закон.
Действительно,
![]()
![]()
|
Подтвердите эти свойства физическими примерами. |
Здесь мы воспользовались свойством линейности проекций векторов на ось.
3. ![]() – сочетательный закон относительно скалярного множителя.
– сочетательный закон относительно скалярного множителя.
Оно доказывается просто:
![]()
Вынося скалярный множитель за знак проекции, мы опять применяем свойство линейности.
Отметим, что скалярный квадрат вектора равен квадрату его модуля:
![]()
Получим теперь формулу скалярного произведения в координатной форме. Пусть даны векторы ![]() и
и ![]() , заданные своими координатами в прямоугольной системе координат. Тогда они представимы через координатные орты
, заданные своими координатами в прямоугольной системе координат. Тогда они представимы через координатные орты ![]() ,
, ![]() ,
, ![]() в виде:
в виде:
![]()
Поэтому

Но
![]()
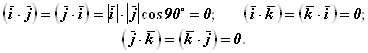
Отсюда следует:
![]() (3.9)
(3.9)
И
![]() (3.10)
(3.10)
Так как
![]() (3.11)
(3.11)
То для нахождения угла между векторами справедливо соотношение:
 (3.12)
(3.12)
Мы получили векторную и координатную формы записи результата, они включают в себя фактически две формулы, каждая из которых имеет самостоятельное значение. В дальнейшем мы будем стараться представлять рабочие формулы именно в таком виде.
|
Докажите, что
|
Для нахождения проекции одного вектора на другой, например,
Получим: |
| < Предыдущая | Следующая > |
|---|
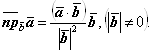
 (3.14)
(3.14)