04.11. еление отрезка в заданном отношении
Деление отрезка в заданном отношении
Введем систему координат. Проще всего было бы связать ее начало с одним из концов отрезка и направить вдоль этого отрезка какую-либо из осей. Однако в реальных условиях приходится решать задачу тогда, когда система координат уже введена, исходя из других упрощающих расчеты предпосылок. Поэтому надо полагать для общности рассуждений, что отрезок задан в системе координат 0xyz своим началом 
и концом 
(рис. 3.31).
На прямой М1М2 требуется найти точку 
, обеспечивающую выполнение соотношения
|
Рис. 3.31. Деление |
Где L – заданное число.
Введем векторы 
, 
и 
. Векторы 
и 
– коллинеарны. Поэтому
= 
Но
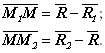
Поэтому
Решая это уравнение относительно вектора 
, будем иметь:
(3.7)
Переходя от векторной формы записи решения задачи к координатной, получим:
(3.8)
Эти формулы выражают координаты точки М.
| < Предыдущая | Следующая > |
|---|
