04.10. Прямоугольная система координат
Прямоугольная система координат
Рассмотрим частный случай аффинной системы координат, у которой координатные оси взаимно перпендикулярны. Такая система координат называется прямоугольной. Базисные векторы в этом случае обозначаются через ![]() ,
, ![]() и
и ![]() , считая
, считая ![]() первым,
первым, ![]() – вторым,
– вторым, ![]() – третьим вектором, и называются их ортами, а соответствующие им оси назовем 0x, 0y, 0z.
– третьим вектором, и называются их ортами, а соответствующие им оси назовем 0x, 0y, 0z.
Напомним, что
![]() .
.
Выделяют правую и левую системы координат. Система координат и сама координатная тройка называются ПРАВОЙ (ЛЕВОЙ) (рис. 3.29), если из конца вектора ![]() поворот от вектора
поворот от вектора ![]() к вектору
к вектору ![]() на кратчайший угол виден как поворот, осуществляемый против часовой стрелки (по часовой стрелке).
на кратчайший угол виден как поворот, осуществляемый против часовой стрелки (по часовой стрелке).

А) б)
Рис. 3.29. Прямоугольная система координат:
а) правая, б) левая.
На практике чаще всего используется правая система координат. Применение левой системы координат обычно оговаривается.
Нами была уже доказана теорема о разложении вектора по трем некомпланарным направлениям. Оказывается, ее применение в прямоугольной системе координат позволяет связать координаты вектора с его проекциями на координатные оси.
ТЕОРЕМА 7. Координаты вектора ![]() (х, у, z) являются его проекциями на оси в прямоугольной системе координат.
(х, у, z) являются его проекциями на оси в прямоугольной системе координат.
ДОКАЗАТЕЛЬСТВО. Пусть дан произвольный вектор ![]() . Введем систему координат, связав начало отсчета с началом этого вектора, и построим параллелепипед, проводя через точку М – конец вектора–плоскости, параллельные координатным плоскостям (рис. 3.30). По теореме о разложении вектора по трем некомпланарным направлениям будем иметь:
. Введем систему координат, связав начало отсчета с началом этого вектора, и построим параллелепипед, проводя через точку М – конец вектора–плоскости, параллельные координатным плоскостям (рис. 3.30). По теореме о разложении вектора по трем некомпланарным направлениям будем иметь:
![]() .
.
Но векторы ![]() ,
, ![]() и
и ![]() являются векторными проекциями и связаны с ортами
являются векторными проекциями и связаны с ортами ![]() соотношениями:
соотношениями:
![]() ,
,
Где х, у и z – координаты вектора ![]() , а также точки М – конца этого вектора.
, а также точки М – конца этого вектора.
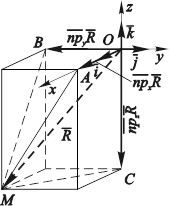
Рис. 3.30. Связь между координатами и проекциями
векторов.
Благодаря введению прямоугольной системы координат удается легко решать многие задачи. И от того, насколько удачно она введена, зависит успех их решения. При решении задач мы сумеем в этом неоднократно убедиться.
Воспользуемся методом координат для доказательства линейных свойств проекции вектора на ось. Пусть даны векторы ![]() , скаляры
, скаляры ![]() и ось L. Докажем, что
и ось L. Докажем, что
![]()
Действительно, введем систему координат так, чтобы ось L и ось Oх совпали. Пусть
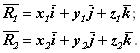
Очевидно, что

Тогда

Коэффициент при орте ![]() есть координата по оси OX вектора
есть координата по оси OX вектора ![]() . Но он же и является
. Но он же и является ![]() . Поэтому
. Поэтому
![]()
Отметим, что если ось L не связывать с какой-либо из осей координат, то доказательство этого свойства усложнится. Оно также усложнится и при геометрическом подходе к доказательству.
| < Предыдущая | Следующая > |
|---|