04.09. Векторная и скалярная проекции вектора

Векторная и скалярная проекции вектора

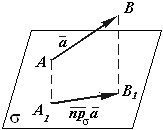
Проектирование различных линий и поверхностей на плоскость позволяет построить наглядное изображение предметов в виде чертежа. Будем рассматривать прямоугольное проектирование, при котором проектирующие лучи перпендикулярны плоскости проекции. ПРОЕКЦИЕЙ ВЕКТОРА НА ПЛОСКОСТЬ считают вектор = (рис. 3.22), заключенный между перпендикулярами, опущенными из его начала и конца.

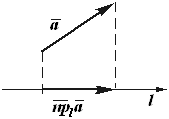Рис. 3.22. Векторная проекция вектора на плоскость.

Рис. 3.23. Векторная проекция вектора на ось.

В векторной алгебре часто приходится проектировать вектор на ОСЬ, то есть на прямую, имеющую определенную ориентацию. Такое проектирование выполняется легко, если вектор и ось L лежат в одной плоскости (рис. 3.23). Однако задача усложняется, когда это условие не выполнено. Построим проекцию вектора на ось, когда вектор и ось не лежат в одной плоскости (рис. 3.24).

Рис. 3.24. Проектирование вектора на ось
в общем случае.

Докажите, что при параллельном переносе векторов их векторная проекция не изменится.

Через концы вектора проводим плоскости, перпендикулярные прямой L. В пересечении с этой прямой данные плоскости определяют две точки А1 и B1 – вектор , который будем называть векторной проекцией данного вектора. Задача нахождения векторной проекции может быть решена проще, если вектор приведен в одну плоскость с осью, что возможно осуществить, так как в векторной алгебре рассматриваются свободные векторы.

Наряду с векторной проекцией, существует и СКАЛЯРНАЯ ПРОЕКЦИЯ, которая равна модулю векторной проекции, если векторная проекция совпадает с ориентацией оси L, и равна величине, ей противоположной, если векторная проекция и ось L имеют противоположную ориентацию. Скалярную проекцию будем обозначать:

Векторная и скалярная проекции не всегда терминологически разделяются строго на практике. Обычно пользуются термином «проекция вектора», подразумевая под этим скалярную проекцию вектора. При решении же задач необходимо четко эти понятия различать. Следуя установившейся традиции, будем использовать термины «проекция вектора», подразумевая скалярную проекцию, и «векторная проекция» – в соответствии с установленным смыслом.

Докажем теорему, позволяющую вычислять скалярную проекцию заданного вектора.

ТЕОРЕМА 5. Проекция вектора на ось L равна произведению его модуля на косинус угла между вектором и осью, то есть

(3.5)

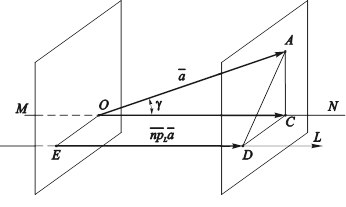
Рис. 3.25. Нахождение векторной и скалярной
Проекций вектора на ось L
( и ось L одинаково ориентированы).

ДОКАЗАТЕЛЬСТВО. Выполним предварительно построения, позволяющие найти угол G Между вектором и осью L. Для этого построим прямую MN, параллельную оси L и проходящую через точку О – начало вектора (рис. 3.25). Угол и будет искомым углом. Проведем через точки А и О две плоскости, перпендикулярные оси L. Получим:

Так как ось L и прямая MN параллельны.

Выделим два случая взаимного расположения вектора и оси L.

1. Пусть векторная проекция и ось L одинаково ориентированны (рис. 3.25). Тогда соответствующая скалярная проекция .

2. Пусть и L ориентированы в разные стороны (рис. 3.26).

Рис. 3.26. Нахождение векторной и скалярной проекций вектора на ось L ( и ось L ориентированы в противоположные стороны).

Тогда

.

Таким образом, в обоих случаях справедливо утверждение теоремы.

ТЕОРЕМА 6. Если начало вектора приведено к некоторой точке оси L, и эта ось расположена в плоскости s, вектор образует с векторной проекцией на плоскость s угол , а с векторной проекцией на ось L – угол , кроме того сами векторные проекции образуют между собой угол , то

. (3.6)

ДОКАЗАТЕЛЬСТВО. Треугольники ОАВ, ОВС и ОАС – прямоугольные, поэтому

Рис. 3.27. Вектор и его векторные проекции на плоскость S и ось L, лежащую в этой плоскости
(И ось L одинаково ориентированы).

Сформулируйте и докажите эту теорему, когда не все углы A, B Обязательно острые (рис 3.28).

Доказанная теорема важна не только в векторной алгебре, но актуальна и при решении многих стереометрических задач.

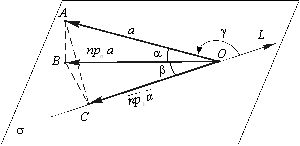
Рис. 3.28. Вектор и его векторные проекции
На плоскость S и ось L, лежащую в этой плоскости
(И ось L противоположно ориентированы).

 

< Предыдущая		Следующая >