04.08. Понятие системы координат
Понятие системы координат
|
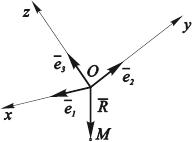
Рис. 3.21. Аффинная |
Теорема о разложении вектора по трем некомпланарным направлениям позволяет аналитически описать положение вектора в пространстве. Три некомпланарных, а значит, линейно независимых вектора 
и 
образуют БАЗИС – систему векторов, через которые может быть выражен любой другой вектор пространства как их линейная комбинация. Базис еще называют РЕПЕРОМ пространства. Параллельным переносом приведем эти векторы к общему началу. С каждым из них можно связать одинаково ориентированную с ним ось. Эти оси и образуют в общем случае так называемую АФФИННУЮ СИСТЕМУ КООРДИНАТ (рис. 3.21). Еще во времена Р. Декарта координатные оси было принято обозначать x, y, z. Сейчас довольно часто используют буквенные обозначения с индексами, что позволяет добиться компактной записи и удобства составления программ для ЭВМ.
Если в репере 
справедливо разложение произвольного вектора 
, имеющее вид:
То числа 
называют КООРДИНАТАМИ ВЕКТОРА и обозначают: 
Отметим, что указание координат вектора вовсе не фиксирует жестко его положение в пространстве. Координаты вектора лишь отражают его аналитическую связь с базисом, задающим систему координат. Мы рассматриваем свободные векторы, и любой вектор, полученный из данного путем параллельного переноса, будет иметь те же координаты.
Однако в том случае, когда рассматриваются векторы, приведенные к началу отсчета, их концы однозначно определяют положение соответствующих точек пространства. Вот почему координаты вектора 
считаются координатами точки М, а сам вектор – ее радиусом-вектором. Это позволяет сформулировать важный принцип аналитической геометрии: Всякой точке пространства, в которой введена аффинная система координат, соответствует тройка чисел – ее координаты, и, наоборот, каждому набору трех координат соответствует определенная точка пространства. Более подробно с этим принципом мы познакомимся ниже.
Возможность разложения вектора по двум неколлинеарным направлениям позволяет путем аналогичных рассуждений ввести и аффинную систему координат на плоскости.
ТЕОРЕМА 4. Если 
и 
– произвольные векторы в базисе , то их линейная комбинация 
является вектором 
, координаты которого – линейные комбинации соответствующих координат данных векторов.
ДОКАЗАТЕЛЬСТВО. Представим векторы 
и 
в виде их разложения по базису:
(3.3)
(3.4)
Умножая первое равенство на A, второе на B И складывая их почленно, получим
,
Что и доказывает теорему.
Из доказанной теоремы следуют простые правила, определяющие линейные операции над векторами в координатной форме.
Правило 1. Чтобы сложить (вычесть) два вектора, нужно сложить (вычесть) их соответствующие координаты.
Правило 2. Чтобы умножить (поделить) вектор на число, необходимо умножить (поделить) на это число его координаты.
| < Предыдущая | Следующая > |
|---|
