04.04. Линейные операции над векторами

Линейные операции над векторами

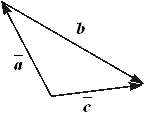
Вектор называется СУММОЙ ВЕКТОРОВ и , если он соединяет начало вектора с концом вектора при условии, что начало приведено паралельным переносом к концу (рис. 3.7)


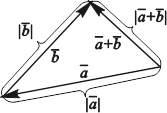
Рис. 3.7. Сложение векторов.	Рис. 3.8. Правило Многоугольника.

При каких условиях сложение векторов по данному правилу даст результат, совпадающий с результатом сложения в соответствии с предпринятой попыткой введения этого действия?

Если же число слагаемых больше двух, то справедливо ПРАВИЛО МНОГОУГОЛЬНИКА: вектор называется суммой векторов если он соединяет начало вектора с концом вектора в предположении, что начало каждого последующего вектора соединено с концом предыдущего (рис. 3.8).

Покажите геометрически справедливость этих свойств.

Очевидно, что правило параллелограмма является частным случаем вышеприведенного. Легко убедиться, что введенное подобным образом сложение векторов удовлетворяет переместительному и сочетательному законам.

Введенное правило сложения векторных величин имеет важное следствие: модуль суммы векторов не превосходит суммы их модулей, т. е.

В каком случае будет достигаться знак равенства? Сохранится ли это неравенство, если число векторов больше двух?

Оно вытекает из известных геометрических соотношений в треугольнике (рис. 3.9).

Рис. 3.9. Модуль суммы векторов.

При всей простоте данных свойств их применение на практике не всегда очевидно. Рассмотрим задачу.

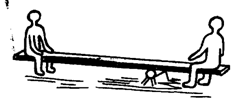
Два человека разного веса качаются на качелях (рис. 3.10, а). Где следует расположить опору качелей, чтобы ни один из качающихся их «не перетягивал», то есть, качели должны расположиться горизонтально, если оба человека не раскачиваются и не задевают ногами землю. Решим данную задачу методом математического моделирования. Рассмотрим физическую модель задачи (рис. 3.10, б). Объектом исследования является расположение места опоры качелей, на которых сидят два человека разного веса. Будем считать качели недеформируемым стержнем, располагающимся на точечной опоре, к концам которого приложены силы веса первого и второго человека. Следует найти равнодействующую этих сил. Она и позволит определить искомую реакцию опоры.

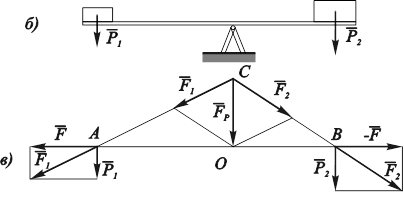
Рис. 3.10. Выбор места опоры качели.

Введем математическую модель. Пусть отрезок AB есть недеформируемый стержень (рис. 3.10, в). К концам AB приведены векторы и , которые соответствуют силам веса качающихся людей. Требуется найти точку пересечения прямой, на которой располагается равнодействующая, с отрезком AB. Данные векторы по физическому смыслу задачи не являются свободными (это – скользящие векторы), поэтому их приведение к общему началу невозможно. Вместе с тем, силы и имеют равнодействующую. Найдем ее, пользуясь искусственным приемом. Дополним данную систему векторов вектором , приложенным к точке A и лежащим на прямой AB, а также вектором , приложенным к точке B. Сумма векторов и равна нулю, поэтому новая система векторов равносильна исходной. Но Отсюда . Перемещая векторы и вдоль соответствующих прямых их действия, получим в пересечении точку С. Из геометрических соображений следует, что || || .