04.03. Действия над векторами

Действия над векторами

В действиях над векторами можно выделить две группы операций: одни из них похожи на некоторые арифметические действия – другие имеют специфические особенности. Первую группу называют линейными операциями. Она включает в себя сложение и вычитание векторов, а также умножение вектора на скаляр. Вторая группа охватывает действия, характерные лишь для векторных величин – скалярное произведение, векторное произведение и различные виды смешанных произведений.

Введение действий над векторами – важный этап в формировании векторной алгебры как научной теории. Дело в том, что эти действия обязаны удовлетворять по меньшей мере двум критериям:

1. Было бы желательно, чтобы они имели как можно больше общих свойств с алгебраическими действиями над числами.

2. В них необходимо наиболее полно отразить свойства объектов окружающего мира.

Легко ли эти требования выполнить? Попробуем ввести, например, сложение векторов, руководствуясь, казалось бы, вполне разумными соображениями. Будем считать вектор суммой векторов и , если угол между и делится этим вектором пополам, а его модуль равен (рис. 3.5, а). Проверим, будут ли выполняться свойства действия сложения, имеющие место для действительных чисел.

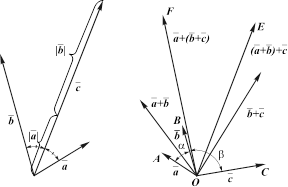
А) б)

Рис. 3.5. Возможный вариант выполнения действия
сложения векторов.

Переместительный закон, очевидно, окажется справедлив:

.

Проверим, выполняется ли равенство:

 – сочетательный закон сложения.

Пусть даны три вектора приведенные к общему началу 0 (рис. 3.5, б). Обозначим известные углы:

Тогда

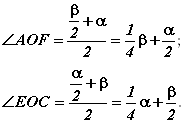
Рис. 3.6. Сложение сил по правилу параллелограмма.

Это означает, что, если , то сочетательный закон выполняться не будет. Еще более существенным возражением против такого введения действия сложения векторов является то, что в механике, например, суммой сил и , действующих в точке О, является вектор  – диагональ параллелограмма, выходящая из точки О (рис. 3.6).

Следовательно, по указанному выше правилу вводить сложение векторов нецелесообразно.

 

< Предыдущая		Следующая >