04.02. Понятие вектора
Понятие вектора
Любая прямая на плоскости или в пространстве задает определенное направление, на котором различают две взаимно противоположные ориентации. Зададим на этой прямой две точки А и В. Будем считать А начальной точкой, а В – конечной. Полученный ориентированный отрезок АВ прямой мы назовем вектором (рис. 3.1).
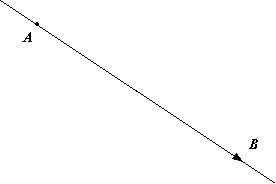
Рис. 3.1. Вектор ![]() .
.
Данное определение, впрочем, не является единственным. Вектор можно определить и как упорядоченную пару точек на координатной плоскости или, аналогично, в пространстве. За каждым из этих определений стоят математические подходы к изучению объектов окружающего мира. В дальнейшем мы покажем связь данных определений и возможные их обобщения, применяемые в современной математике.
Принято называть МОДУЛЕМ вектора длину задающего его ОТРЕЗКА. Вектор, начало и конец которого совпадают, называется нулевым вектором, его модуль равен нулю, а ориентация не определена. При обозначении векторных величин сверху ставится горизонтальная черта, например: ![]() ; модули векторов обозначаются как
; модули векторов обозначаются как ![]() . Нулевой вектор обозначается числом ноль.
. Нулевой вектор обозначается числом ноль.
Векторы считаются РАВНЫМИ, если они имеют равные модули и одинаковую ориентацию. При всей простоте этого определения его применение на практике вызывает вопросы. Из него следует, что равные векторы можно переносить параллельно самим себе (от этого не изменятся их модули и ориентация). Однако в действительности подобные переносы не всегда допустимы.
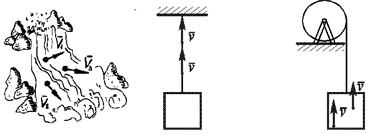
Пусть, например, ![]() – скорость частицы воды горного водопада (рис. 3.2) в какой-то момент времени. Едва ли можно утверждать, что скорость потока в любой другой точке будет та же. По физическому смыслу этот вектор нельзя переносить в другую точку пространства. Такие векторы называются ПРИЛОЖЕННЫМИ.
– скорость частицы воды горного водопада (рис. 3.2) в какой-то момент времени. Едва ли можно утверждать, что скорость потока в любой другой точке будет та же. По физическому смыслу этот вектор нельзя переносить в другую точку пространства. Такие векторы называются ПРИЛОЖЕННЫМИ.
|
|
Если теперь ![]() – скорость троса какого-либо сечения, равномерно поднимающего груз (рис. 3.3), то перенос этого вектора вдоль прямой действия силы натяжения вполне возможен. Такие векторы называются СКОЛЬЗЯЩИМИ.
– скорость троса какого-либо сечения, равномерно поднимающего груз (рис. 3.3), то перенос этого вектора вдоль прямой действия силы натяжения вполне возможен. Такие векторы называются СКОЛЬЗЯЩИМИ.
|
Рис. 3.2. |
Рис. 3.3. |
Рис. 3.4. |
Если же, наконец, ![]() – скорость кабины лифта (рис. 3.4), то вектор может быть перенесен в любую ее точку. Скорость остается неизменной по модулю и ориентации. Такие векторы называются СВОБОДНЫМИ.
– скорость кабины лифта (рис. 3.4), то вектор может быть перенесен в любую ее точку. Скорость остается неизменной по модулю и ориентации. Такие векторы называются СВОБОДНЫМИ.
|
Приведите примеры физических процессов, описываемых приложенными, скользящими и свободными векторами. |
Класс равных векторов – СВОБОДНЫЙ ВЕКТОР.
| < Предыдущая | Следующая > |
|---|