03.14. Нахождение расстояния от точки до прямой на плоскости и от точки до плоскости
Нахождение расстояния от точки до прямой на плоскости и от точки до плоскости
Эти две задачи аналогичны по своей постановке и решению. Ограничимся рассмотрением одной из них. Расстояние от точки до прямой определяется длиной перпендикуляра, проведенного к прямой из заданной точки. Глядя на различные типы уравнений прямой на плоскости, мы должны выбрать такое ее задание, при котором удается решить поставленную задачу более просто. Попробуем применить нормальное уравнение прямой (4.27), поскольку параметр р тоже характеризует расстояние от одной из точек – начала координат, до данной прямой. Итак, пусть дана точка 
и прямая 
(рис. 4.22).
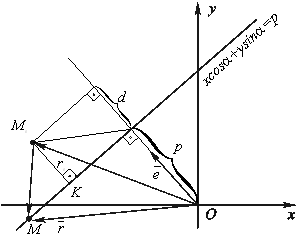
Рис. 4.22. Нахождение расстояния от точки до прямой.
Длина отрезка M0K, перпендикулярного прямой, и есть искомое расстояние d. Рассмотрим радиусы-векторы 
, а также 
, связанный с произвольной точкой данной прямой. Тогда искомое расстояние d будет равно 
, где 
– единичный вектор нормали к прямой. Проекцию приходится брать по модулю, потому что знак ее зависит от того, находятся ли точка M0 и начало координат по одну сторону от прямой или по разные. В нашем случае векторная проекция
Ориентирована в противоположную сторону по отношению к вектору , поэтому соответствующая скалярная проекция отрицательна. Проводим очевидные преобразования:
.
Итак, расстояние от точки до прямой, заданной нормальным уравнением, находится по формуле:
.
6. Формула вычисления расстояния от точки 
до плоскости
Имеет вид:
.
Докажите эту формулу. Продумайте, каким должен быть чертеж, отражающий наиболее выразительно постановку и решение задачи.
7. Какой будет формула вычисления расстояния от точки до прямой на плоскости при использовании других типов уравнений прямой?
8. Найти уравнение прямой на плоскости, проходящей через точку 
Под углом 
к прямой, заданной нормальным уравнением
.
9. Найти нормальное уравнение прямой, проходящей через точки 
.
10. Найти полярное уравнение прямой, проходящей через точки .
11. Найти точку пересечения непараллельных прямых на плоскости, когда их уравнения заданы:
А) в полярной системе координат;
Б) в отрезках;
В) в нормальном виде.
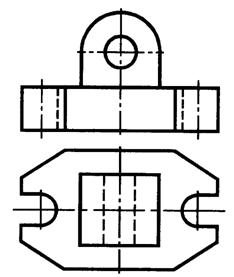
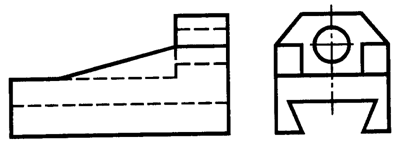
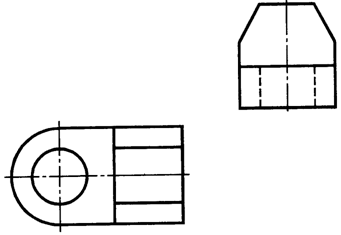
12. По двум заданным видам детали (рис. 4.23) постройте третий вид, применив необходимые разрезы. Выполните технический рисунок детали. Опишите аналитически линии на чертежах и плоскости на техническом рисунке, введя требуемые размеры.
|
|
||
|
|
||
|
|
Рис. 4.23. Заданные виды детали.
| < Предыдущая | Следующая > |
|---|
