03.13. Уравнение плоскости, проходящей через
Уравнение плоскости, проходящей через
три заданные точки
Эта задача однозначно разрешима, если точки не лежат на одной прямой. В противном случае она не имеет
единственного решения. Пусть в прямоугольной системе координат 0xyz заданы три точки: ![]()
![]()
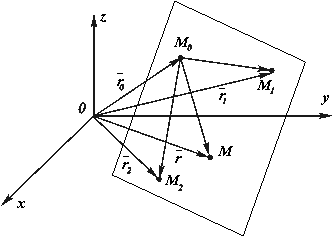
![]() не лежащие на одной прямой, через которые проходит данная плоскость (рис. 4.21). Пусть
не лежащие на одной прямой, через которые проходит данная плоскость (рис. 4.21). Пусть ![]() – произвольная точка этой плоскости.
– произвольная точка этой плоскости.
|
Рис. 4.21. Задание плоскости тремя точками,
не лежащими на одной прямой
Для точек плоскости и только для них векторы ![]()
![]() и
и ![]() компланарны. Но
компланарны. Но
![]()
Где ![]() – радиусы-векторы точек M, M0, M1, M2.
– радиусы-векторы точек M, M0, M1, M2.
Необходимым и достаточным условиям компланарности трех векторов является равенство нулю их смешанного произведения. Поэтому равенство
![]()
Или
![]()
Можно считать векторным уравнением плоскости, проходящей через три данные точки. В координатной форме оно может быть записано компактно следующем образом:
 .
.
| < Предыдущая | Следующая > |
|---|