03.10. Прямая в пространстве

Прямая в пространстве

Рассмотрим различные типы уравнений прямой в пространстве. Пусть в системе координат 0xyz известна точка , через которую проходит данная прямая и направляющий вектор , которому она параллельна (рис. 4.18).

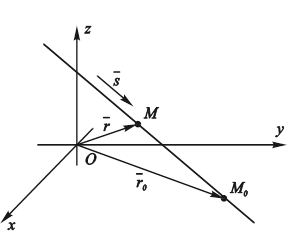
Рис. 4.18. Задание прямой параметрическими
уравнениями.

Рассмотрим произвольную точку , лежащую на ней. Введем в рассмотрение векторы и , приведенные к началу отсчета. Для точек прямой и только для них векторы и будут коллинеарны, поэтому они будут связаны зависимостью:

Где t – некоторый числовой параметр, или

. (4.35)

Это есть векторно-параметрическое уравнение прямой. В проекциях на координатные оси оно приводит нас к трем координатно-параметрическим уравнениям:

(4.36)

Придавая параметру t различные значения, мы будем получать координаты x, y и z точек, лежащих на прямой.

Выразим параметр t из каждого уравнения:

 –

Какие возможны изменения параметров x0, y0, z0, l, m и n, при которых данное геометрическое место точек останется неизменным?

Откуда

. (4.37)

Эти уравнения называются каноническими уравнениями прямой. Их два (но не три!). Очевидно, что всякое третье равенство, выводимое из (4.37), будет следствием двух других.

Известно, что если плоскости:

(4.38)

Непараллельны, т. е. их нормальные векторы и неколлинеарны:

То плоскости пересекаются.

Систему уравнений (4.38) можно рассматривать как уравнения прямой, заданной в виде пересечения двух плоскостей.

Связь между уравнениями (4.37) и (4.38) достаточно очевидна. Некоторые трудности может вызвать переход от уравнений (4.38) к уравнениям (4.37). Чтобы получить последние уравнения, необходимо найти координаты какой-либо точки прямой Х0, y0, z0 и координаты направляющего вектора прямой l, m, n. Это можно сделать следующим образом. Пусть система (4.38) совместна, тогда фиксируем какую-либо из переменных в уравнениях плоскостей и решаем полученные два уравнения с двумя неизвестными.

Рис. 4.19. Направляющий вектор прямой, заданной
пересечением плоскостей и .

Полученные значения x0, y0, и z0 будут координатами искомой точки прямой. Направляющий вектор прямой находим, исходя из того, что он должен быть перпендикулярен (рис. 4.19) обоим нормальным векторам и . Поскольку направляющим вектором прямой может быть взят любой ненулевой вектор, ей параллельный, то примем:

Всегда ли возможно решить систему (4.38) и почему?

.

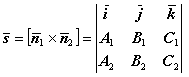Возможен ли какой-либо иной прием перехода от уравнений прямой, заданной в виде пересечения двух плоскостей, к каноническим?

Это позволит получить канонические уравнения прямой.

Очевидно, что одна и та же прямая может быть задана пересечением различных плоскостей. Мы приходим к интересному факту: одно и то же геометрическое место точек может описываться не только разными типами уравнений, но даже в рамках одного типа эти уравнения могут быть различны.

Рассмотрим, например, описание оси 0х в пространстве.

Ее векторно-параметрическое уравнение имеет вид:

Где направляющий вектор может быть для простоты взят равным орту , то есть этот вектор теперь будет задан так: За точку, лежащую на прямой, примем начало координат. В координатно-параметрическом виде это уравнение распадается на три уравнения:

Канонические уравнения оси 0x, очевидно, примут вид:

Деление на нуль имеет символический смысл.

 

< Предыдущая		Следующая >