03.08. Общее уравнение плоскости

Общее уравнение плоскости

Общее уравнение плоскости выводится аналогично общему уравнению прямой. Пусть в прямоугольной системе координат 0xyz известны: точка , через которую проходит заданная плоскость, и вектор , ей перпендикулярный, называемый НОpмальным вектоpом плоскости (pис. 4.15).

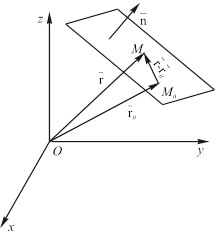
Рис. 4.15. Задание плоскости общим уравнением.

Задание этих характеристик однозначно определяет положение плоскости в пространстве. Пусть – произвольная точка плоскости. Рассмотрим приведенные к началу отсчета векторы и . Для точек плоскости и только для них вектор

Будет перпендикулярен нормальному вектору, условием чего является равенство нулю скалярного произведения

Или

. (4.31)

Это есть векторная запись уравнения плоскости. В координатной форме оно будет иметь вид:

Или

(4.32)

Где

Уравнение (4.32) называется общим уравнением плоскости.

Выше установлено, что всякое уравнение первой степени относительно координат x и y задает на плоскости прямую. Аналогичными рассуждениями можно показать, что всякое линейное уравнение относительно x, y и z

Задает плоскость.

Нормальный вектор плоскости позволяет судить о ее расположении по отношению к координатным осям.

Если допустить, что одна из его проекций – нулевая, то нормальный вектор перпендикулярен соответствующей оси, а плоскость будет ей параллельна.

Например, плоскость

Параллельна оси Ох, так как координата нормального вектора А = 0 (рис. 4.16).

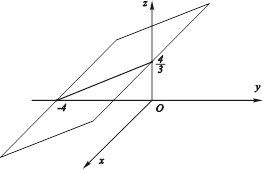
Рис. 4.16. Расположение плоскости
В системе координат 0Xyz.

Если какие-либо две координаты нормального вектора равны нулю, то данная плоскость параллельна двум координатным осям, а значит, и всей координатной плоскости, с ними связанной. Например:

Есть уравнение плоскости, параллельной координатной плоскости 0уz. Для сравнения отметим, что это же самое уравнение на плоскости определяет прямую, параллельную оси 0y.

Если же в уравнении (4.32) свободный член D = 0, то плоскость проходит через начало координат.

Проведенные рассуждения позволяют легко получить уравнения координатных плоскостей:

X = 0 – уравнение плоскости 0уz;

Y = 0 – уравнение плоскости 0xz;

Z = 0 – уравнение плоскости 0xy.

Как и выше, для нахождении угла между произвольными плоскостями

–

Воспользуемся формулой

Плоскости параллельны, если их нормальные векторы коллинеарны:

Где , или в координатной форме

Плоскости будут взаимно перпендикулярны, если будут взаимно перпендикулярны их нормальные векторы, то есть равно нулю скалярное произведение:

Или

Уравнение прямой с угловым коэффициентом имеет вид . Но для плоскости такого типа уравнение специально не вводится. А между тем по аналогии можно рассмотреть, например, уравнение .