03.07. Прямая в полярных координатах

Прямая в полярных координатах

Для вывода уравнения прямой в полярных координатах воспользуемся ее нормальным уравнением:

Заменяя декартовые координаты x и y на полярные и (рис. 4.14) по формулам (4.28), получим:

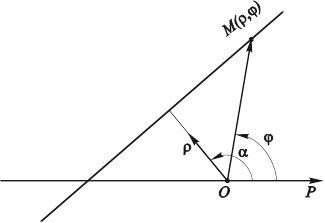
Рис. 4.14. Геометрические характеристики, определяющие положение прямой в полярной системе координат.

(4.29)

Таким образом, если известны угол Между полярной осью OL и нормальным вектором прямой, а также ее расстояние р от начала координат, то по формуле (4.29) можно получить координаты (,) точек, лежащих на прямой, придавая произвольные неотрицательные значения, удовлетворяющие условию

И находя соответствующие значения . Уравнение прямой в полярной системе координат не является линейным, что затрудняет его использование.

Сформулируйте ряд задач, которые решались бы проще именно с использованием уравнения прямой в полярной системе координат?

Очевидно, что условия параллельности прямых осям координат, как и формула угла между двумя прямыми, сохранят тот же самый вид, что и при рассмотрении нормального уравнения прямой, так как параметр имеет неизменный геометрический смысл.

Итак, мы рассмотрели следующие уравнения прямой на плоскости.

I. – уравнение прямой с угловым коэффициентом;

II. – общее уравнение прямой;

III. – векторно-параметрическое уравнение;

IV. 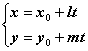– координатно-параметрические уравнения;

V. – каноническое уравнение;

VI. – нормальное уравнение;

VII. – уравнение в полярных координатах.

Переход от одного типа уравнений к другому в некоторых случаях может вызвать трудности. Они преодолимы, если принимается во внимание геометрический смысл параметров, входящих в уравнения. Рассмотрим, например, переход от общего уравнения прямой (II) к нормальному (VI). Если общее уравнение прямой переписать в виде:

То это еще не есть ее нормальное уравнение: A и B могут и не быть координатами единичного нормального вектора, приведенного к началу координат, а величина –C при этом не будет равна расстоянию от прямой до начала координат. Чтобы преодолеть данную трудность, умножим левую и правую части уравнения (II) на некоторый множитель и попробуем его подобрать так, чтобы

Возводя первые два равенства в квадрат и складывая их почленно, будем иметь :

Или

. (4.30)

Знак множителя , который называют нормирующим, выбираем с условием того, что р – расстояние от прямой до начала координат – величина неотрицательная. Он всегда противоположен знаку коэффициента C¹0.

< Предыдущая		Следующая >