03.06. Полярная система координат

Полярная система координат

Положение точек на плоскости может быть задано не только декартовыми координатами. Возможны и другие подходы к их описанию. Полярная система координат является одним из них. Благодаря использованию этой системы, удается гораздо проще аналитически описать многие геометрические места точек и решить эффективнее некоторые задачи.

Введем полярную систему координат следующим образом. Выберем на плоскости (рис. 4.10) произвольную точку О, проведем

Рис. 4.10. Полярная система координат

Луч Ор и назовем его полярной осью, а точку О – полюсом (началом отсчета). Полярными координатами точки М будем считать расстояние от полюса до данной точки и угол , на который нужно повернуть против часовой стрелки луч, лежащий на полярной оси, до совмещения с лучом ОМ. Точка с полярными координатами и обозначается следующим образом: . Для самого полюса О полярный радиус равен нулю, а угол неопределен. Для того, чтобы соответствие между полярными координатами и точками плоскости было взаимно однозначным, полагают, что и изменяются в следующих границах:

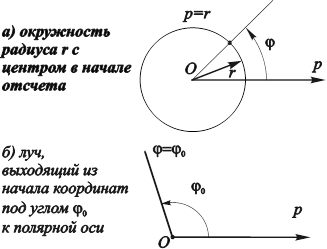
Рассмотрим, например, уравнения окружности и луча, выходящего из полюса, в полярной системе координат. Если центр окружности радиуса R располагается в полюсе 0 (рис. 4.11, а), то ее уравнение имеет вид:

.

Рис. 4.11. Линии, имеющие простейшее описание в полярной системе координат

Действительно, все точки, лежащие на окружности, отстоят на одинаковом расстоянии r от ее центра, поэтому при любом мы всегда будем получать только точки, ей принадлежащие.

Уравнению

Соответствует луч (рис. 4.11, б), проходящий через полюс под углом .

Множество линий:

При различных допустимых значениях констант образуют координатную сетку (рис. 4.12). Один из элементов этой сетки заштрихован.

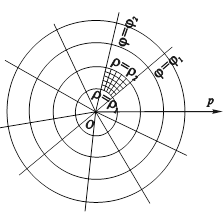
Рис. 4.12. Координатная сетка в полярной системе координат

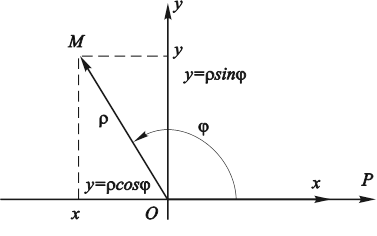
Рис. 4.13. Связь между полярными и декартовыми координатами точки.

Найдем связь между полярными и прямоугольными декартовыми координатами точки. Эта связь легко устанавливается, если полярная и декартовая системы координат имеют общее начало, а полярная ось P совпадает с ориентацией оси 0x (рис. 4.13). Пусть точка M имеет полярные координаты , и декартовые координаты x, y. Тогда очевидны соотношения:

(4.28)

Они позволяют по полярным координатам найти декартовые. Чтобы перейти от декартовых координат к полярным, из равенств (2.28) определим полярный радиус.

Следует ли учитывать значение корня ?

Полярный угол находим по формуле:

При этом следует учитывать, в каком квадранте расположена точка М.

< Предыдущая		Следующая >