03.05. Нормальное уравнение прямой

Нормальное уравнение прямой.

Нормальное уравнение прямой позволяет описать аналитически положение ее точек на плоскости через два параметра: расстояние p от начала прямоугольной системы координат до прямой и угол a, образуемый нормальным вектором прямой с осью абсцисс (рис. 4.8).

Рис. 4.8. Задание прямой нормальным уравнением.

Пусть  – произвольная точка, лежащая на прямой. Наряду с нормальным вектором прямой , рассмотрим его орт . Как известно, проекции единичного вектора на координатные оси Оx и Оy декартовой прямоугольной системы координат равны, соответственно, и , где  – угол, который образует этот вектор с осью Ох, поэтому будет являться единичным нормальным вектором прямой. Для всех точек, лежащих на прямой, и только для них будет справедливо соотношение:

Где  – радиус-вектор произвольной точки прямой.

Но

Поэтому

, (4.26)

А это и есть нормальное уравнение прямой в векторном виде.
В координатной форме оно может быть записано следующим образом:

(4.27)

Отметим, что параметр p, являясь расстоянием от начала координат до прямой, не должен быть отрицательным, а угол a отсчитывается против часовой стрелки.

При или прямая будет параллельна оси 0y; при или прямая параллельна оси абсцисс; при прямая проходит через начало координат.

Если даны две прямые, заданные своими нормальными уравнениями:

То угол между ними (рис. 4.9) равен

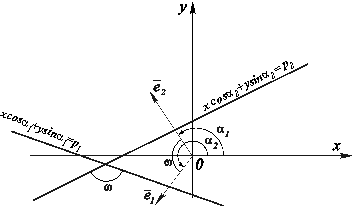
Рис. 4.9. Нахождение угла между прямыми, заданными нормальными уравнениями.

Прямые будут параллельными, если разность будет равна нулю или p. Они окажутся взаимно перпендикулярны, если эта разность примет значения или же .

< Предыдущая		Следующая >