03.04. Параметрические уравнения прямой

Параметрические уравнения прямой.

Описание прямой с помощью параметрических уравнений является еще одним подходом к ее исследованию. Им пользуются довольно часто в механике, где параметр t выступает как время.

Пусть в заданной декартовой прямоугольной системе координат Oхy известна точка (рис. 4.6),

Рис. 4.6. Задание прямой с помощью параметрических уравнений.

Через которую проходит прямая, и дан ненулевой вектор , ей параллельный, который будем называть направляющим вектором.

Рассмотрим произвольную точку , лежащую на прямой, и введем, как и ранее, радиусы-векторы:

И

Тогда вектор

Для точек прямой и только для них будет коллинеарен направляющему вектору

А потому

Где t – числовой параметр, который для каждой определенной точки M, лежащей на прямой, принимает конкретное значение. Переписав это уравнение в виде

(4.21)

Получим ВЕКТОРНО-ПАРАМЕТРИЧЕСКОЕ УРАВНЕНИЕ ПРЯМОЙ. Проектируя вектор (4.21) на координатные оси, найдем координатно-параметрические уравнения прямой:

(4.22)

Могут ли параметрические уравнения не быть линейными относительно параметра t?

В данном случае прямая определяется двумя уравнениями. Задавая конкретные значения t, мы можем вычислить абсциссу и ординату точки прямой.

Выразим из этих уравнений параметр t:

И приравняем правые части полученных равенств:

(4.23)

Это есть каноническое уравнение прямой, где x0 и y0 – координаты известной точки, лежащей на прямой, l и m – координаты направляющего вектора.

Какая-либо из координат этого вектора может обращаться в ноль. Тогда каноническое уравнение имеет символический смысл, так как деление на ноль невозможно.

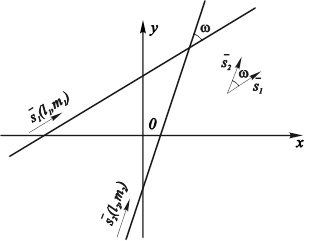
Рис. 4.7. Нахождение угла между прямыми, заданными параметрически.

Параметрические и каноническое уравнения позволяют достаточно просто определить взаимное расположение прямых путем использования соответствующих направляющих векторов. Если этими векторами являются и (рис. 4.7), то

, (4.24)

Или в координатной форме:

(4.25)

 

< Предыдущая		Следующая >