03.03. Общее уравнение прямой
Общее уравнение прямой
Опишем аналитически геометрическое место точек, лежащих на прямой, следующим образом. Пусть в системе координат Оху дана прямая (рис. 4.4).
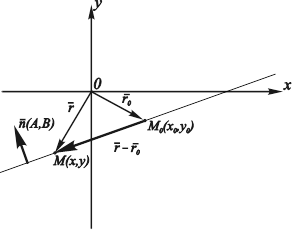
Рис. 4.4. Задание прямой общим уравнением
Назовем ненулевой вектор ![]() , перпендикулярный к ней, нормальным вектором прямой. Будем считать известными координаты точки
, перпендикулярный к ней, нормальным вектором прямой. Будем считать известными координаты точки ![]() , лежащей на прямой. Задание нормального вектора
, лежащей на прямой. Задание нормального вектора ![]() И этой точки M0 однозначно определяет положение прямой на плоскости. Пусть
И этой точки M0 однозначно определяет положение прямой на плоскости. Пусть ![]() – произвольная точка, лежащая на прямой. Свяжем с точками M0 и M радиус-векторы
– произвольная точка, лежащая на прямой. Свяжем с точками M0 и M радиус-векторы ![]() и
и ![]() . Введем в рассмотрение вектор
. Введем в рассмотрение вектор
![]() .
.
Для точек прямой и только для них будет выполняться условие:
![]() .
.
Его мы и положим в основу вывода общего уравнения прямой. Необходимым и достаточным условием взаимной перпендикулярности двух векторов является равенство нулю их скалярного произведения:
![]()
Или
![]()
Раскрывая скобки, получим:
![]() (4.9)
(4.9)
Это есть уравнение прямой в векторной форме. Оно включает в себя известные векторы ![]() и
и ![]() , а также вектор
, а также вектор ![]() , который характеризует положение произвольной точки, лежащей на данной прямой. Другие точки плоскости ему удовлетворять не будут.
, который характеризует положение произвольной точки, лежащей на данной прямой. Другие точки плоскости ему удовлетворять не будут.
Так как
![]()
![]()
То в координатной форме уравнение прямой примет вид:
![]() (4.10)
(4.10)
Или
![]() (4.11)
(4.11)
Где
![]()
Уравнение (4.11) называется общим уравнением прямой.
Таким образом, мы доказали теорему:
Теорема. Всякой прямой на плоскости соответствует линейное уравнение относительно координат ее точек.
Будет ли справедливо обратное утверждение?
Теорема. Любое уравнение первой степени (4.11) относительно переменных x и y в декартовой прямоугольной системе координат Охy определяет прямую.
ДОКАЗАТЕЛЬСТВО
Пусть в уравнении (4.11) хотя бы один из коэффициентов А или В отличен от нуля. В прямоугольной системе координат Оху возьмем какую либо точку ![]() , координаты которой удовлетворяют уравнению (4.11)
, координаты которой удовлетворяют уравнению (4.11)
![]() . (4.12)
. (4.12)
Таких пар чисел существует бесконечно много.
Вычитая из уравнения (4.11) равенство (4.12), получим уравнение (4.10), эквивалентное (4.11). Оно означает, как уже известно, равенство нулю скалярного произведения вектора ![]() и вектора
и вектора ![]() , что возможно только тогда, когда переменные x и y являются координатами точки прямой. Это и доказывает теорему.
, что возможно только тогда, когда переменные x и y являются координатами точки прямой. Это и доказывает теорему.
Общее уравнение прямой без труда приводится к виду (4.1), если ![]() :
:
![]()
При этом ![]() и
и ![]() .
.
Коэффициенты A и B являются координатами нормального вектора к прямой, а потому они позволяют получить представление о ее расположении на плоскости. Если A = 0 и ![]() , то нормальный вектор
, то нормальный вектор ![]() , а прямая параллельна оси абсцисс. Уравнение такой прямой имеет вид:
, а прямая параллельна оси абсцисс. Уравнение такой прямой имеет вид:
![]()
Если ![]() ,
, ![]() , то нормальный вектор
, то нормальный вектор ![]() и данная прямая параллельна оси ординат. Ее уравнение приобретает вид:
и данная прямая параллельна оси ординат. Ее уравнение приобретает вид:
![]()
Именно такая прямая не охватывается множеством прямых, определяемых уравнением (4.1).
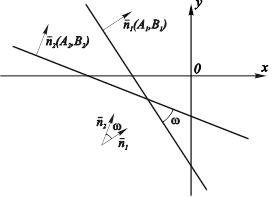
Рис. 4.5. Нахождение угла между прямыми, заданными общим уравнением.
Найдем угол между двумя прямыми (рис. 4.5), заданными общими уравнениями:
![]() (4.13)
(4.13)
![]() (4.14)
(4.14)
По виду уравнений определяем координаты нормальных векторов данных прямых: ![]() ,
, ![]() . Угол между двумя данными прямыми будет равен углу между их нормальными векторами, как углы со взаимно перпендикулярными сторонами, поэтому решение задачи имеет вид:
. Угол между двумя данными прямыми будет равен углу между их нормальными векторами, как углы со взаимно перпендикулярными сторонами, поэтому решение задачи имеет вид:
 . (4.15)
. (4.15)
В координатной форме эти выражения записываются следующим образом:
![]() . (4.16)
. (4.16)
Если прямые параллельны, то их нормальные векторы ![]() и
и ![]() будут коллинеарны, поэтому
будут коллинеарны, поэтому
![]() . (4.17)
. (4.17)
Это равенство определяет условие параллельности прямых в векторном виде. В координатной форме оно будет следующим:
![]() (4.18)
(4.18)
Если прямые взаимно перпендикулярны, то и соответствующие нормальные векторы также перпендикулярны, следовательно, скалярное произведение этих векторов будет равно нулю:
![]() ,
,
Или в координатной форме:
![]() (4.19)
(4.19)
|
Как расположены прямые, у которых
|
Очевидно, что если в уравнениях (4.13) и (4.14) имеет место пропорциональность
![]() (4.20)
(4.20)
То они определяют одну и ту же прямую.
| < Предыдущая | Следующая > |
|---|