03.02. Уравнение прямой с угловым коэффициентом
Уравнение прямой с угловым коэффициентом
Положение прямой на плоскости может быть однозначно задано различными путями. Они определяют не только разнообразие подходов к изучению свойств прямых, но и позволяют оптимальным образом выбрать способ решения конкретных задач с учетом известных исходных данных и провести его исследование.
Известно, что уравнение прямой на плоскости с угловым коэффициентом может быть задано в виде:
![]() , (4.1)
, (4.1)
Где k – угловой коэффициент прямой, равный тангенсу угла, образованного прямой с положительным направлением оси Ох, а b – ордината точки пересечения прямой с осью y.

Рис. 4.2. Задание прямой уравнением с угловым
коэффициентом.
Всякая ли прямая на плоскости может быть представлена этим уравнением? Всегда ли удобно пользоваться им при решении разнообразных задач? Возможны ли другие формы представления прямой на плоскости? Эти и другие вопросы мы будем обсуждать, развивая возможности описания геометрического места точек, задающих прямую.
Значения параметров k и b позволяют однозначно судить о расположении прямой на плоскости. Очевидно, если ![]() , т. е.
, т. е. ![]() и
и ![]() (исходя из геометрического смысла задачи, нет
(исходя из геометрического смысла задачи, нет
Необходимости рассматривать все множество значений ![]() ,
, ![]() , при которых
, при которых ![]() ), то прямая проходит параллельно оси Ох:
), то прямая проходит параллельно оси Ох:
![]()
Есть уравнение такой прямой.
При ![]() прямая проходит через начало координат и имеет уравнение
прямая проходит через начало координат и имеет уравнение
![]() .
.
Если в уравнении (4.1) коэффициенты k и b одновременно равны нулю, то оно принимает вид :
![]()
И задает ось 0х.
Уравнение вида (4.1), вместе с тем, не позволяет выделить путем подбора коэффициентов k и b какую-либо прямую, параллельную оси 0y, так как угол, образуемый с осью 0x, для любой такой прямой равен ![]() и
и ![]() не существует. Эту трудность в дальнейшем удастся преодолеть при рассмотрении других уравнений прямой.
не существует. Эту трудность в дальнейшем удастся преодолеть при рассмотрении других уравнений прямой.
Рассмотрим некоторые задачи, которые решаются достаточно просто при использовании уравнения (4.1).
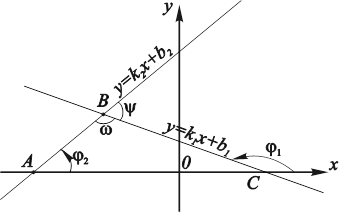
Рис. 4.3. Нахождение угла между прямыми, заданными уравнениями с угловыми коэффициентами.
Найдем угол между двумя прямыми (рис. 4.3), заданными уравнениями:
![]() (4.2)
(4.2)
![]() (4.3)
(4.3)
Коэффициенты k1 и k2 позволяют найти углы ![]() и
и ![]() , которые образуют эти прямые с осью Ох.
, которые образуют эти прямые с осью Ох.
Тогда ![]() – один из возможных углов между прямыми, находим из
– один из возможных углов между прямыми, находим из ![]() (рис. 4.3):
(рис. 4.3):
![]()
Таким образом,
![]() (4.4)
(4.4)
Из формулы (4.4) следует, что, если
![]() (4.5)
(4.5)
То ![]() – значит, данные прямые параллельны или же совпадают.
– значит, данные прямые параллельны или же совпадают.
Формулу для вычисления угла между прямыми можно представить и в другом виде. Так как
![]()
То
![]() (4.6)
(4.6)
Отсюда
![]() (4.7)
(4.7)
Если в этой формуле поменять ролями коэффициенты k1 и k2 (что приведет к смене знака аргумента арктангенса), то мы определим другой угол ![]() , смежный по отношению к углу
, смежный по отношению к углу ![]() .
.
Полученная формула при
![]()
Дает уже известное условие параллельности прямых, так как при этом
![]()
Если же
![]() , (4.8)
, (4.8)
То прямые перпендикулярны (теперь ![]() ).
).
| < Предыдущая | Следующая > |
|---|