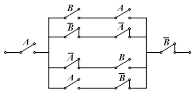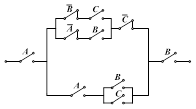02.4. Задачи и размышления
Задачи и размышления
Применения математической логики разнообразны. Она позволяет из отдельных фактов, сведений, наблюдений обоснованно построить новую научную теорию. Рассмотрим, однако, менее глобальные проблемы, решение которых связано с успехами математической логики.
Еще в 1910 году русский физик П. С. Эрнфест сумел увидеть в новой науке – математической логике – великолепный инструмент для исследования контактных схем. Оказалось, что между алгеброй высказываний и работой контактных схем можно провести аналогии: высказывания могут быть истинны (1) или же ложны (0) – контакты, соответственно, замкнуты (1) или разомкнуты (0). Конъюнкции и дизъюнкции высказываний А и В соответствуют схеме, состоящей из последовательного и параллельного соединения замыкающих контактов А и В (рис. 2.2).
|
Высказывание А (контакт А) |
Высказывание В (контакт В) |
Высказывание АÙВ (последовательное соединение контактов) |
Высказывание АÚВ (параллельное соединение контактов) |
|
|
|
1 1 0 0 |
1 0 1 0 |
1 0 0 0 |
1 1 1 0 |
Рис. 2.2. Соответствие между соединением контактов и алгеброй
Высказываний.
Отрицанию высказывания А, т. е. высказыванию ![]() , ставится в соответствие размыкающий контакт. Если А обозначает замыкающий контакт, то при его срабатывании в цепи идет ток. При срабатывании размыкающего контакта
, ставится в соответствие размыкающий контакт. Если А обозначает замыкающий контакт, то при его срабатывании в цепи идет ток. При срабатывании размыкающего контакта ![]() ток в цепи прекращается.
ток в цепи прекращается.
|
Рис. 2.3. Размыкающий контакт. |
Для размыкающего контакта примем обозначение, указанное на рис. 2.3.
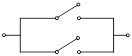
Контактные схемы стараются упростить путем уменьшения числа контактов при сохранении электрической эквивалентности. Связь с алгеброй высказываний позволяет обоснованно выполнять эти преобразования. Например, контактная схема, изображенная на рисунке 2.4 а, эквивалентна более простой (рис. 2.4 б), так как структура контактных связей для данной схемы имеет вид:
А) исходная контактная схема;
Б) упрощенная контактная схема;
|
|
|
|
А) |
Б) |
Рис. 2.4. Упрощение контактной схемы
![]()
И может быть с помощью известных тавтологий упрощена до выражения: ![]() . Ему и соответствует схема, приведенная на рис. 2.4 б.
. Ему и соответствует схема, приведенная на рис. 2.4 б.
1. Упростить контактные схемы, изображенные на рис. 2.5, заменив их эквивалентными.
|
|
|
|
A) |
Б) |
Рис. 2.5. Контактные схемы, подлежащие упрощению.
2. Разработать контактную цепь, моделирующую импликацию ![]() .
.
3. Построить контактные цепи, математическими моделями которых являются рассмотренные тавтологии 1-23.
Мы уже хорошо представляем роль ЭВМ в жизни современного общества. Конструкция вычислительной машины и принципы ее работы – это результат достижений многих наук. Двоичная система, использующая цифры 1 и 0, наиболее удобна для представления чисел в ЭВМ. Именно она лучше всего реализуется через электрические, оптические, магнитные и другие системы передачи информации.
В двоичной системе число представляется в виде
![]()
Где ![]() выражают цифру 0 или 1.
выражают цифру 0 или 1.
Например, число 77 в двоичной системе имеет вид 1011001. Благодаря использованию двоичной системы, удалось сконструировать функциональные элементы, которые позволяют осуществлять как алгебраические операции над числовыми величинами, так и логические операции над высказываниями.
Развитие идей математической логики продвинуло решение многих проблем теории алгоритмов. АЛГОРИТМ – это система формальных правил, с помощью которых решаются задачи определенного типа. Простейшие алгоритмы появились еще в глубокой древности. Узбекский математик IX в. до н. э. аль-Хорезми разработал правила четырех арифметических действий над числами в десятичной системе. С его именем и связано слово «алгоритм». Вам хорошо знаком алгоритм Евклида для нахождения наибольшего общего делителя двух чисел. Но, оказывается, не для всех задач удается найти алгоритм решения.
В 1900 году на Международном конгрессе математиков Д. Гильберт выдвинул 23 проблемы, относящиеся к различным областям математики, как особо важных для ее развития.
|
Математика – удивительная наука. Доказать, что задача неразрешима – в этой науке крупный успех. Дать «всего лишь» определение – путь к открытию новых истин. Такое возможно, пожалуй, только в математике. |
Сравнительно недавно, в 1970 году, математика ознаменовалась важным событием. Была доказана алгоритмическая неразрешимость в целых числах уравнения ![]() где P – многочлен произвольной степени с целыми коэффициентами от неизвестных X1,...xn. Тем самым решена знаменитая 10-я проблема Д. Гильберта. Данный результат получил двадцатилетний аспирант Ленинградского университета Юрий Матиясевич. Это оказалось возможным благодаря точному математическому определению алгоритма, основанному на достижениях математической логики. Оно было сформулировано в тридцатых годах нашего столетия крупными учеными А. А. Марковым и П. С. Новиковым, внесшими серьезный вклад в современную математику.
где P – многочлен произвольной степени с целыми коэффициентами от неизвестных X1,...xn. Тем самым решена знаменитая 10-я проблема Д. Гильберта. Данный результат получил двадцатилетний аспирант Ленинградского университета Юрий Матиясевич. Это оказалось возможным благодаря точному математическому определению алгоритма, основанному на достижениях математической логики. Оно было сформулировано в тридцатых годах нашего столетия крупными учеными А. А. Марковым и П. С. Новиковым, внесшими серьезный вклад в современную математику.
Разработка программного обеспечения для современных ЭВМ все более приближает нас к тому, что в ближайшее время существенно сократится дистанция между алгоритмом задачи и условностями алгоритмического языка.
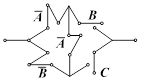
4. Используя логические операции, составить алгоритм и различные варианты программ для ЭВМ, реализующих идею попадания точки в заштрихованные области.
 Рис. 2.6. Области, в которые ожидается попадание точки.
Рис. 2.6. Области, в которые ожидается попадание точки.
5. Вычислить значение многочлена
![]()
Где ![]() – числовые коэффициенты, n – степень многочлена, при
– числовые коэффициенты, n – степень многочлена, при ![]() .
.
Вычисления можно сделать путем непосредственной подстановки числа a в многочлен, а можно и путем подстановки этого числа в преобразованный многочлен:
![]()
Составить алгоритмы вычисления значения многочлена и реализовать их на ЭВМ с использованием логических операторов. Оценить эффективность каждого из путей решения задачи с точки зрения алгоритмической простоты и требуемого числа операций для их выполнения.
Интересно заметить: идеи математической логики оказываются полезными в раскрытии преступлений. Вот одна из уже классических задач «детективного жанра», взятая у французского писателя Ж. Сименона.
6. «Вернувшись домой, Мегрэ позвонил на набережную Орфер.
- Говорит Мегрэ. Есть новости?
- Да, шеф. Поступили сообщения от инспекторов. Торранс установил, что если Франсуа был пьян, то либо Этьен не убийца, либо Франсуа лжет. Жуссье считает, что или Этьен убийца, или Франсуа не был пьян, и убийство совершено после полуночи. Инспектор Люка просил передать Вам, что если убийство произошло после полуночи, то либо Этьен убийца, либо Франсуа лжет. Затем звонила….
- Все. Спасибо. Этого достаточно. – Комиссар положил трубку. Он знал, что трезвый Франсуа никогда не лжет. Теперь он знал все».
К какому же выводу пришел комиссар Мегрэ?
Попробуйте разработать контактную цепь, моделирующую «логику преступления».
Придумайте подобные задачи сами и решите их.
7. А. М. Горькому принадлежат слова: «Знать необходимо не затем, чтобы только знать, но для того, чтобы делать».
Другими словами: знание необходимо для того, чтобы делать что-то полезное. Можно ли считать это условие и достаточным; необходимым и достаточным?
8. Опишите процесс решения уравнения ![]() с помощью алгебры предикатов.
с помощью алгебры предикатов.
9. На выборах президента банка баллотировались два кандидата. Бюллетень для тайного голосования имеет вид
Иванов А. Б. за против
Петров В. Г. за против
Ненужное зачеркнуть
Допускается ли по данной формуле двойное толкование?
Составьте алгоритм и программу подсчета результатов голосования.
Математическая логика открыла перспективу для новых исследований, развивая формализованный стиль построения научных теорий. Их формализованный стиль явился основой оригинальных научных теорий. К началу XX века математическая логика стала уже классической наукой. Порой казалось, что возможности ее безграничны. Но в 1931 году была доказана знаменитая теорема Геделя, согласно которой мир не может быть описан одним лишь формальным языком, основанным на конечном числе аксиом. Стало ясно, что полная формализация научного знания неосуществима. Однако пытливый ум ученых с не меньшим интересом создает новые научные направления: вероятностную логику, модальную логику, семантическую логику. Разрабатываются интуиционистская и конструктивная логики. Аппарат математической логики гармонично включается в кибернетику, квантовую механику, нейрофизиологию и другие прикладные науки, обогащая их новыми идеями.
| < Предыдущая | Следующая > |
|---|