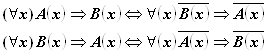02.3. Структура теоремы. Виды теорем

Структура теоремы. Виды теорем

Известно, что ТЕОРЕМА – это высказывание в теории, имеющее доказательство (то есть истинное в данной теории). Доказательство опирается на аксиомы, определения и другие теоремы. ТЕОРЕМА является формулой, выводимой в рамках построенной аксиоматической системы. При формулировке теоремы мы стараемся распространить определенное свойство на целую группу предметов или явлений, т. е. показать, что Любой объект из этой группы обладает отмеченной особенностью. Обычно теорема состоит из условия и заключения, которые связаны между собой логической операцией – импликацией. Вот почему, с точки зрения логической структуры, любая теорема есть высказывание вида:

Допустимы ли выражения: «Данная теорема неверна», «Проверим справедливость теоремы», «Эта теорема недоказуема»?

Это высказывание назовем ПРЯМОЙ ТЕОРЕМОЙ.

Используя правило контрпозиции, дадим определение.

Теорема

Называется противоположной обратной для прямой теоремы (таблица 8а). Если при этом теоремой является высказывание , то оно называется обратной теоремой, а теорема

Называется противоположной теоремой. В этом случае имеет место следующий список теорем (табл. 8Б.)

Таблица 8а.

Тип теоремы	Логическая формула
Прямая
Противоположная обратной

Таблица 8б.

Тип теоремы	Логическая формула
Прямая
Обратная
Противоположная
Противоположная обратной

Таблица 8. Виды теорем и связь между ними.

Прямая и обратная теоремы связаны с понятиями НЕОБХОДИМОГО И ДОСТАТОЧНОГО УСЛОВИЙ. В прямой теореме присутствуют два предиката и , один из которых определяет Условие, другой – Вывод теоремы. В обратной теореме условие и вывод меняются местами. Поэтому, рассматривая прямую и обратную теоремы, предикаты и будем называть условиями. Если имеет место прямая теорема, то называют ДОСТАТОЧНЫМ УСЛОВИЕМ ДЛЯ , а  – НЕОБХОДИМЫМ УСЛОВИЕМ ДЛЯ . Если же имеет место обратная теорема, то НАЗЫВАЮТ НЕОБХОДИМЫМ УСЛОВИЕМ ДЛЯ , а  – ДОСТАТОЧНЫМ УСЛОВИЕМ ДЛЯ . Если, наконец, справедливы импликации, то есть , то условие НАЗЫВАЮТ НЕОБХОДИМЫМ И ДОСТАТОЧНЫМ УСЛОВИЕМ ДЛЯ .

Но ежели для истинной любви страдание всегда необходимо, То, видно, уж таков закон любви, Научимся сносить его с терпением. Шекспир. Итак, страдание – необходимое условие истинной любви. Можно ли считать это условие и достаточным?

В сущности, необходимое условие есть условие, истинность которого следует из истинности некоторого другого утверждения. Достаточное условие есть условие, из истинности которого следует истинность некоторого другого утверждения. Необходимое и достаточное условие есть соединение двух вышерассмотренных условий. Для его формулировки используют также словосочетания: «… тогда и только тогда …», «… в том и только в том случае …», «… если и только если …».

Следует различать противоположную теорему

И отрицание прямой теоремы

Из свойств кванторных операций следует:

.

Используя тавтологии 22 и 23, прямую теорему можно представить в виде:

А ее отрицание – следующим образом:

Эти соотношения полезны для понимания сути высказываний, определяющих прямую теорему и ее отрицание.

Редкий случай в математике: способом для иллюстрации рассуждений служат сами теоремы. Обычно бывает наоборот.

Рассмотрим примеры.

ТЕОРЕМА ВИЕТА. Если приведенное квадратное уравнение

Имеет корни Х1 и Х2, то

Введем предикаты : «Приведенное квадратное уравнение A: имеет корни х1 и х2» и : «В приведенном квадратном уравнении A Числа х1 и х2 удовлетворяют соотношениям:

».

Содержание теоремы определяется высказыванием

Считая эту теорему прямой, сформулируем обратное высказывание: , то есть

Если числа х1 и х2 таковы, что

То х1 и х2 – корни квадратного уравнения:

Как известно, оно является теоремой:.

В силу существования обратной теоремы сформулируем противоположную теорему: .

ТЕОРЕМА. Если в приведенном квадратном уравнении

Числа х1 и х2 не являются корнями, то Хотя бы одно из равенств:

Выполняться не будет.

Теорему, противоположную обратной, сформулируем следующим образом:

ТЕОРЕМА. Если числа х1 и х2 таковы, что Хотя бы одно из равенств:

Не выполняется, то х1 и х2 не будут корнями квадратного уравнения

Она возможна, так как имеет место прямая теорема.

Прямая теорема может быть еще сформулирована на основании тавтологии 22 иначе.

ТЕОРЕМА. Или Хотя бы одно из чисел х1 и х2 не является корнем приведенного квадратного уравнения

Или

Сформулируем отрицание прямой теоремы: «Неверно, что если приведенное квадратное уравнение

Имеет корни х1 и х2, то

.

Данное высказывание ложно, так как имеет место прямая теорема. Из тавтологии 23 следует, что оно эквивалентно следующему: «Существует такое приведенное квадратное уравнение

Что х1 и х2 – его корни и Хотя бы одно из равенств

Не выполняется.

Прямая и обратная теоремы, могут быть объединены в одну.

ТЕОРЕМА. Для того, чтобы действительные числа х1 и х2 были корнями приведенного квадратного уравнения

,

Необходимо и достаточно, чтобы выполнялись условия:

Рассмотрим еще одну теорему.

ТЕОРЕМА. Диагональ параллелограмма делит его на два равных треугольника.

Введем предикаты : «Четырехугольник  – параллелограмм» и : «Диагональ делит четырехугольник на два равных треугольника». Тогда можно утверждать, что если четырехугольник – параллелограмм (предикат ), то этого условия достаточно для того, чтобы диагональ параллелограмма делила его на два равных треугольника. Сформулируем обратное высказывание.

«Если диагональ четырехугольника делит его на два равных треугольника, то этот четырехугольник – параллелограмм.

Оно неверно, что подтверждает контрпример на рис. 2.1. Поэтому условие не может быть необходимым, а  – достаточным.

Рис. 2.1. Контрпример к обратной теореме.

 

< Предыдущая		Следующая >