02.2. Предикаты

Предикаты

В математике часто рассматриваются предложения, зависящие от одной или нескольких переменных. Например, предложение A: «|X|=X». Оно не является высказыванием, так как о его истинности либо ложности нельзя ничего сказать без знания конкретного значения Х: для Х<0 Оно ложно, для остальных – истинно.

Предложение, содержащее переменные, которые при замене их на возможные значения становится высказыванием, называется предикатом, или высказывательной формой.

Предложение A(x): «|X|=X» можно считать предикатом одной переменной. Предикат А(х), зависящий от одной переменной, называется одноместным.

Совокупность значений переменной х, которая может не обязательно иметь числовую природу, называется Областью определения предиката. Значения х, обеспечивающие истинность предиката, называются его МНОЖЕСТВОМ ИСТИННОСТИ.

Например, предикат «» является ТОЖДЕСТВЕННО ИСТИННЫМ на множестве действительных х, а предикат «» ТОЖДЕСТВЕННО ЛОЖНЫМ также при всех действительных х.

Предикаты и с одной и той же областью определения называются РАВНОСИЛЬНЫМИ, если они имеют одинаковые множества истинности. Их обозначают: . Например, предикаты «» и «», заданные для действительных х, имеют одинаковое множество истинности , поэтому .

Рассмотрим другое высказывание : «Движение разрешено, если горит х свет светофора». Переменная х принимает значения: «красный», «желтый», «зеленый». И лишь последнее значение «зеленый» определяет множество истинности предиката. Мы видим, что х – не обязательно числовая переменная.

В целом, предикат выражает определенное свойство предмета, явления или выражения, которые служат областью определения логической функции , принимающей значения истинно или ложно. Предикат становится высказыванием тогда, когда переменная х принимает фиксированное значение.

Пусть и  – предикаты с некоторой общей частью области определения переменной х. Будем называть предикат СЛЕДСТВИЕМ предиката , если множество истинности предиката является частью множества истинности предиката . Например, из равенства следует, что , но не наоборот: из равенства не следует, что . Множеством истинности предиката : «» – является единственное значение среди всех действительных чисел, но множество истинности предиката : «», имеющего ту же область определения, содержит бесконечно много значений х, задаваемых формулой среди которых есть и . Это означает, что предикат  – следствие предиката .

Можно утверждать: ПРЕДИКАТЫ и , имеющие одну и ту же область определения, РАВНОСИЛЬНЫ ТОГДА И ТОЛЬКО ТОГДА, КОГДА ЕСТЬ СЛЕДСТВИЕ и ЕСТЬ СЛЕДСТВИЕ .

Существует и ДВУМЕСТНЫЙ предикат . Это более сложная структура. Двуместные предикаты называют еще БИНАРНЫМИ ОТНОШЕНИЯМИ. Например, неравенство можно рассматривать как двуместный предикат , принимающий значение «истинно» для тех пар значений х и у, для которых оно верно, и – «ложно» при х и у, не обеспечивающих выполнение этого неравенства.

Над предикатами возможны те же логические операции, что и над высказываниями: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция. Введем эти операции, рассматривая для определенности одноместные предикаты.

ОТРИЦАНИЕМ ПРЕДИКАТА называется предикат, обозначаемый , с той же областью определения, имеющий следующий смысл: превращается в истинное высказывание при тех х, для которых ложно, и в ложное высказывание при х, для которых высказывание истинно.

Например, пусть даны предикат : «Движение разрешено при х свете светофора», где переменная х принимает значения «красный», «желтый», «зеленый». Предикат станет истинным высказыванием, когда х примет значение «зеленый»; при других х предикат будет определять ложные высказывания. Предикат : «Движение не разрешено при х свете светофора» имеет ту же область допустимых значений переменной х, а его значение истинности будет достигаться при значениях «желтый», «красный».

Другой пример: если предикат : «», то предикат : «». Однако, если предикат означает «», то предикат может лишь означать «».

КОНЪЮНКЦИЕЙ ПРЕДИКАТОВ и , имеющих общую область определения Х, называется предикат, обозначаемый , который превращается в истинное высказывание для тех значений х, при которых оба предиката являются истинными высказываниями.

Например, пусть дан предикат : «Команда N вышла в финал турнира по математическому моделированию» и предикат : «Команда N победила в соревнованиях по лыжным гонкам». Пусть для первого предиката Переменная N принимает натуральные значения на множестве N1 от 1 до 8 включительно, для второго предиката переменная N изменяется на множестве значений N2: 1, 2, 4, 5, 6, 7 и 8 (команда №3 не участвовала в лыжных гонках). Пусть команды №2 И №5 – финалисты турнира из восьми команд по математическому моделированию, а команда №2 победила в соревнованиях семи команд по лыжным гонкам. Тогда предикат , определенный на множестве N2 (общая часть множеств N1 и N2) будет представлять собой истинное высказывание, когда . Другой пример. Конъюнкцией предикатов : «» и : «», определенных на множестве действительных чисел, будет предикат , который окажется истинным высказыванием для .

Приведите свой пример, иллюстрирующий это определение.

ДИЗЪЮНКЦИЕЙ ПРЕДИКАТОВ и , имеющих общую область определения Х, называется предикат, обозначаемый: , который превращается в истинное высказывание для тех значений х, при которых Хотя бы один предикат является истинным высказыванием.

Конъюнкция и дизъюнкция предикатов, возможно не всегда осознанно, используются нами при решении уравнений и неравенств. Например, отыскание решения системы уравнений

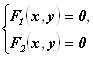
Есть задача нахождения общего множества истинности предикатов «» И «» В их общей области определения, т. е. конъюнкции этих предикатов.

Если же дано уравнение

То его решение есть множество истинности предикатов «» Или «» в их общей области определения, то есть дизъюнкцией этих предикатов.

В случае решения неравенства

Требуется объединить множества решений двух систем:

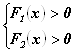и -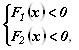

Что означает по отношению к предикатам «», «», «» и «» следующие логические операции:

.

ИМПЛИКАЦИЕЙ ПРЕДИКАТОВ и , имеющих общую область определения Х, называется предикат, обозначаемый , который превращается в ложное высказывание для тех значений х, при которых первый предикат является истинным высказыванием, а второй – ложным.

Например, предикат , образованный из предикатов : «» и : «», будет ложным для . И при всех остальных х он будет истинным.

ЭКВИВАЛЕНЦИЕЙ ПРЕДИКАТОВ и , имеющих общую область определения Х, называется предикат, обозначаемый , который превращается в истинное высказывание для тех значений х, при которых оба предиката превращаются одновременно либо в истинное, либо в ложное высказывание.

Например, предикаты «» и «» эквивалентны на множестве действительных чисел, так как области истинности и ложности каждого из них совпадают. Предикаты «» и «» не являются эквивалентными на этом множестве, так как области их истинности и ложности не совпадают, но они будут эквивалентны, если из этого множества исключить точку , так как .

Решим неравенство

Используя логические операции в проводимых преобразованиях:

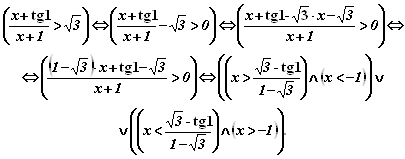В полученной дизъюнкции предикатов первый предикат

Всегда ли справедлива эквиваленция

Ложный, второй

Истинный. Таким образом, решением задачи будет второй предикат.

Рассмотрим теперь кванторные операции, специфические для предикатов, не имеющие аналогов среди операций над высказываниями.

КВАНТОРОМ ВСЕОБЩНОСТИ называется операция, по которой предикату ставится в соответствие высказывание, обозначаемое , которое истинно тогда и только тогда, когда предикат тождественно истинен. Высказывание читается: «Для любого х справедливо ».

Например, для предиката «», заданного на множестве действительных чисел, квантор всеобщности означает: для любого х справедливо неравенство . Это высказывание будет истинным, так как предикат тождественно истинный.

Если предикат , заданный на множестве действительных чисел, означает «», то высказывание «» будет ложным, потому что данный предикат не является тождественно истинным, так как при он определяет ложное высказывание.

КВАНТОРОМ СУЩЕСТВОВАНИЯ называется операция, по которой предикату ставится в соответствие высказывание, обозначаемое , которое ложно тогда и только тогда, когда предикат тождественно ложен. Высказывание читается: «Существует такое х (хотя бы одно), что справедливо ».

Например, для предиката : «», заданного на множестве действительных чисел, квантор существования означает: существует такое х, что справедливо неравенство . Это высказывание будет ложным, так как предикат тождественно ложный.

Если предикат , заданный на множестве действительных чисел, означает «», то высказывание Будет истинным, так как предикат не является тождественно ложным. Существует бесконечно много значений х, для которых высказывание «» будет истинным.

Если предикат определен на множестве, состоящем из конечного числа элементов , то квантор всеобщности можно трактовать как конъюнкцию всех возможных из него высказываний, а квантор существования – как дизъюнкцию этих высказываний:

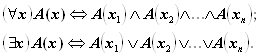
Справедливы эквиваленции:

В дальнейшем мы будем использовать эти соотношения при доказательстве теорем.

< Предыдущая		Следующая >