2.10. Предельные теоремы в схеме Бернулли

Если число испытаний П Велико, то вычисления по формуле Бернулли становятся затруднительными. В то же время большие значения П Позволяют заменять эту формулу приближенными асимптотическими формулами. Рассмотрим три такие формулы.

Теорема 2.5. (Формула Пуассона) Если так, что , то

(2.5)

Формула (2.5) дает хорошие результаты, если Npq<9. Если же Npq>9, то для вычисления вероятности можно воспользоваться локальной теоремой Лапласа.

Теорема 2.6. (Локальная теорема Муавра–Лапласа). Вероятность появления события Т раз в П независимых испытаниях при больших значениях П приближенно определяется по формуле

(2.6)

Где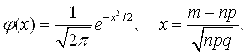

Теорема 2.7. (Интегральная теорема Муавра–Лапласа). Вероятность того, что число появлений события в П независимых испытаниях находится в пределах Т1£ т £ т2 и при больших значениях П приближенно определяется по формуле

(2.7)

Где

Функция Ф(Х) называется Функцией Лапласа. Для функций имеются таблицы ее значений. Функция является четной, а функция Ф(Х) – нечетной, т. е. ; Ф(– Х)= – Ф(Х);

Из интегральной теоремы Лапласа можно вывести формулу для вероятности отклонения относительной частоты Т/п События в серии испытаний от постоянной вероятности Р этого события в одном испытании:

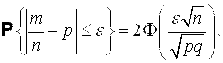(2.8)

Пример 2.21. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0.002. Найти вероятность того, что в пути будут повреждены три изделия.

Решение. Можно считать, что имеем дело со схемой Бернулли, в которой испытания проводятся 500 раз. Так как число П=500 достаточно велико, а вероятность P=0.002 мала (причем Npq=500×0.002×0.998»2<9), то воспользуемся приближенной формулой (2.5), где L=Np =500×0.002=1:

Пример 2.22. Найти вероятность того, что событие происходит 80 раз в 400–х испытаниях, если вероятность этого события в каждом испытании равна 0.2.

Решение. Здесь П=400 достаточно велико, но величина Npq также велика (Npq=400×0.2×0.8=64>9), поэтому воспользуемся формулой (2.6). Вычисляем

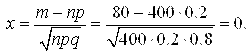
По таблице функции находим (0)=0.3989. Окончательно получаем:

Пример 2.23. Найти вероятность того, что в 400–х испытаниях событие произойдет не более 70–ти раз, если вероятность появления этого события в каждом испытании равна 0.2.

Решение. Воспользуемся интегральной теоремой Лапласа для вычисления вероятности :

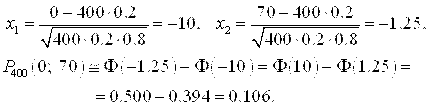
Пример 2.24. Определим, сколько надо провести испытаний, чтобы с вероятностью 0.95 относительная частота выпадения «орла» отличалась от вероятности Р=0.5 этого события не более чем на 5%.

Решение. Воспользуемся формулой (2.8). В нашем случае Р=0.5, Q=0.5, e=0.5 0.05=0.025. По условию задачи

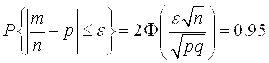
Или Пользуясь таблицей функции Лапласа, по значению функции находим значение аргумента:

т. е.

Отсюда находим, что П=1536.64. Таким образом, надо провести не менее чем 1537 испытаний.

< Предыдущая		Следующая >