30.5. Обоснование привлекательности проекта по выпуску продукции

Для финансирования проектов по строительству и наладке изготовления конкурентоспособной продукции в большинстве случаев фирмам требуются инвестиции. Включение в проект материалов с оптимизацией сетевых моделей в части обоснова­ния сроков возврата инвестиций делает проект более привле­кательным и способствует принятию инвестором положитель­ного решения.

Пример 1. Предприятие решило для улучшения финансового состояния наладить выпуск конкурентоспособной продукции (мороженого). Для переоборудования цеха (участка) под вы­пуск этой продукции необходимо выполнить:

1) подготовку технического задания на переоборудование участка (30 дн.);

2) заказ и поставку нового оборудования (60 дн.);

3) заказ и поставку нового электрооборудования (50 дн.);

4) демонтаж старого и установку нового оборудования (90 дн.);

5) демонтаж старого и установку нового электрооборудо­вания (80 дн.);

6) переобучение персонала (30 дн.);

7) испытания и сдачу в эксплуатацию оборудования для производства мороженого (20 дн.).

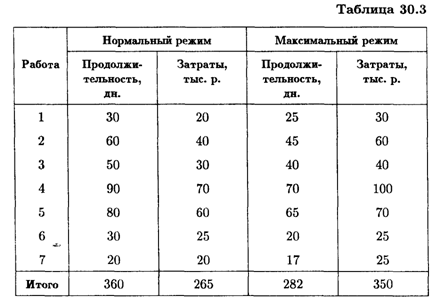
Ожидается, что производительность после ввода новой ли­нии составит 20 т мороженого в смену. Прибыль от реализации 1 т продукции составит 0,5 тыс. р. в смену. Деньги на покуп­ку и переоборудование участка в размере 2000 тыс. р. взяты в банке под 20% годовых (из расчета 1500 тыс. р. на закупку оборудования и 500 тыс. р. на работы по демонтажу старого оборудования и установке нового оборудования). Затраты на проведение работ в нормальном и максимальном режимах ука­заны в табл. 30.3.

Определить, через какое время может быть возвращен кре­дит в банк.

Решение. 1. Составим график проведения работ по пуску новой линии:

На проведение переоборудования необходимо

2. График можно улучшить, выполняя некоторые работы параллельно. Получим график (рис. 30. 14).

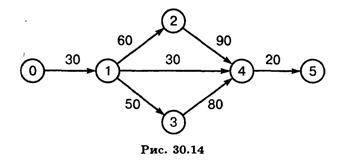
На этом графике обозначены работы:

0,1 — подготовка технического задания;

1,2 — заказ и поставка нового оборудования;

1,3 — заказ и поставка нового электрооборудования;

2,4 — установка нового оборудования;

3,4 — установка нового электрооборудования;

1,4 — переобучение персонала;

4,5 — сдача в эксплуатацию новой линии.

По графику путь (0,1), (1,2), (2,4), (4,5) имеет продолжи­тельность 200 дн.; (0,1), (1,3), (3,4), (4,5) — 180 дн.; (0,1), (1,4),(4,5) - 80дн.

Критическим путем графика является путь, на котором на­ходятся работы (0,1), (1,2), (2,4), (4,5) продолжительностью

30 + 60 + 90 + 20 = 200 дн.

График улучшился на 360 — 200 = 160 дн.

Определим, через какое время после начала выпуска моро­женого может быть возвращен кредит в банк.

Через 200 дн. после начала работ предприятие истратит 1 500 тыс. р. на приобретение оборудования (согласно условию примера) и 265 тыс. р. на его установку и сдачу в эксплу­атацию (см. табл. 30.3, столбец "Затраты" при нормальном режиме). В наличии у предприятия останется

2 000 - 1500 - 265 = 235 тыс. р.

Построим графики изменения кредита в зависимости от времени получения прибыли предприятием — от выпуска мо­роженого (рис. 30.15).

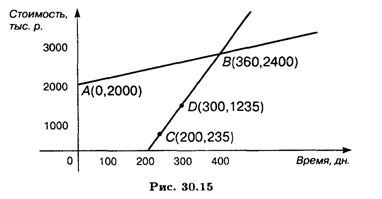
Для построения графика изменения кредита в зависимос­ти от времени составим уравнение. Через 360 дн. после выда­чи банком кредита под 20% годовых долг предприятия соста­вит 2 400 тыс. р. Поэтому известны две точки этой прямой: А (0, 2000), B (360, 2400). Согласно уравнению прямой, прохо­дящей через две точки:

Решая уравнение, получим

Найдем уравнение прибыли предприятия. Известно, что че­рез 200 дн. после начала работ у предприятия осталось от кре­дита 235 тыс. р. Через 100 дн. после начала выпуска продукции предприятие получит прибыль

И у него будет в наличии

Таким образом, для нахождения уравнения прибыли имеем две точки: С (200, 235), D (300, 1235). Тогда

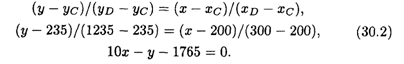
Решая совместно уравнения (30.1) и (30.2), определим вре­мя, когда кредит может быть возвращен в банк:

Откуда получаем У = 2471, Х = 423,6 ≈ 424 дн.

3. График выполнения работ может быть сжат за счет вы­полнения некоторых операций в максимально интенсивном ре­жиме.

Вычислим наклоны кривой "затраты-продолжительность" для каждой операции. Результаты расчетов даны в табл. 30.4.

Учитывая наклоны кривой, производим сжатие операций (0,1), (2,4), (3,4), (4,5), получим сетевой график (рис. 30.16).

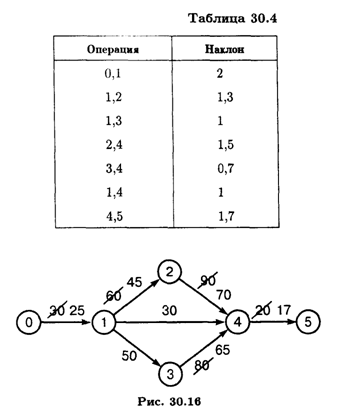
Новый график имеет 2 критических пути: (0,1), (1,2), (2,4), (4,5) и (0,1), (1,3), (3,4), (4,5) с продолжительностью 157 дн.

Таким образом, критический путь сокращен с 200 до 157 дн., а это означает, что предприятие начнет производить мороженое через 157 дн. после начала работ.

Определим, сколько предприятию придется заплатить за "сжатие" критического пути (см. табл. 30.3):

Таким образом, "сжатие" работ (0,1), (1,2), (2,4), (3,4), (4,5) обойдется предприятию в

График изменения кредита в зависимости от времени оста­ется прежним (см. рис. 30.15). Его вид определяет уравнение

Найдем уравнение прибыли.

Через 157 дн. после начала работ у предприятия осталось от кредита

Через 100 дн. после начала выпуска продукции предприя­тие получит прибыль

И у него будет в наличии

Таким образом, для нахождения уравнения прибыли пред­приятия имеем две точки:

Согласно уравнению прямой, проходящей через 2 точки, получим

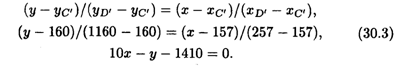
Решая совместно уравнения (30.1) и (30.3), определим вре­мя, когда кредит может быть возвращен в банк:

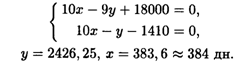
Таким образом, через 384 дн. предприятие может вернуть кредит в банк. По сравнению с предыдущим случаем (см. п. 2) предприятие вернет в банк деньги раньше на 424 — 384 = 40 дн.

При нормальном режиме работ критический путь состав­ляет 200 дн., стоимость работ — 265 тыс. р.

Критический путь уменьшен до 157 дн., минимальная сто­имость работ составляет 265 + 75 = 340 тыс. р. при максималь­ном режиме.

< Предыдущая		Следующая >