30.2. Расчет временных параметров сетевого графика

Основным временным параметром сетевого графика явля­ется продолжительность критического пути.

Расчет критического пути включает два этапа. Первый на­зывается прямым проходом. Вычисления начинают с исходного события и продолжают до тех пор, пока не будет достигнуто завершающее событие. Для каждого события определяется од­но число, представляющее ранний срок его наступления. На втором этапе, называемом обратным проходом, вычисления на­чинают с завершающего события и продолжают, пока не будет достигнуто исходное событие. Для каждого события вычисля­ется поздний срок его наступления.

Рассмотрим прямой проход:

TiР. н. — ранний срок начала всех операций, выходящих из события I.

Если I = 0, то T0р. н. = 0;

TjР. н. — ранний срок начала всех операций, входящих в J.

Тогда

Где Tij — продолжительность операции (I,J);

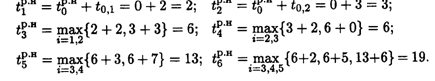
Прямой проход закончился, начинаем обратный:

TiП. o — поздний срок окончания всех операций, входящих в событие I.

Если I = П, где П — завершающее событие сети, то TnП. o = TnР. н. и является отправной точкой обратного прохода;

TiП. о = (TjП. о - Ti,J) для всех операций (I,J);

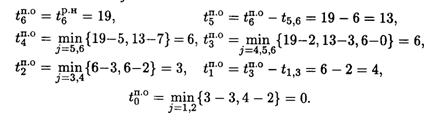
Используя результаты вычислений при прямом и обрат­ном проходах, можно определить операции критического пу­ти. Операция (i, J) принадлежит критическому пути, если она удовлетворяет условиям:

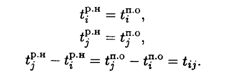
Для рассматриваемого примера критический путь включа­ет операции (0,2), (2,3), (3,4), (4,5), (5,6).

Операции связаны еще с двумя сроками:

TijП. н. — поздний срок начала работы. Он является наибо­лее поздним (максимальным) из допустимых моментов начала данной работы, при котором еще возможно выполнение всех последующих работ в установленный срок:

TijР. o — ранний срок окончания работы. Он является наибо­лее ранним (минимальным) из возможных моментов окончания работы при заданной продолжительности работ:

Различают два вида резервов времени: полный резерв (RП) и свободный резерв (RСв).

Полный резерв времени показывает, на сколько может быть увеличена сумма продолжительности всех работ относитель­но критического пути. Он представляет собой разность между максимальным отрезком времени, в течение которого может быть выполнена операция, и ее продолжительностью (Tij) и определяется как

Свободный резерв времени — максимальное время, на ко­торое можно отсрочить начало или увеличить продолжитель­ность работы при условии, что все события наступают в ран­ние сроки:

Результаты расчета критического пути и резервов време­ни некритических операций представлены в нижеследующей таблице. Следует отметить, что критические операции долж­ны иметь нулевой полный резерв времени, при этом свободный резерв также должен быть равен нулю.

< Предыдущая		Следующая >