29.2.2. Оптимальное распределение ресурсов

Пусть имеется некоторое количество ресурсов Х, которое необходимо распределить между П различными предприяти­ями, объектами, работами и т. д. так, чтобы получить мак­симальную суммарную эффективность от выбранного способа распределения.

Введем обозначения: Xi — количество ресурсов, выделен­ных I-му предприятию (I = );

GI(xi) — функция полезности, в данном случае это величи­на дохода от использования ресурса Xi, полученного I-М пред­приятием;

Fk(X) — наибольший доход, который можно получить при использовании ресурсов Х от первых K различных предприя­тий.

Сформулированную задачу можно записать в математи­ческой форме:

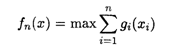
При ограничениях:

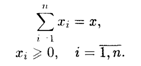
Для решения задачи необходимо получить рекуррентное соотношение, связывающее Fk(X) и Fk-1(X).

Обозначим через Хk количество ресурса, используемого K-М способом (0 ≤ Xk ≤ Х), тогда для (k — 1) способов остается ве­личина ресурсов, равная (X — Xk). Наибольший доход, который получается при использовании ресурса (X — Xk) от первых (K — 1) Способов, составит Fk-1(X — XK).

Для максимизации суммарного дохода от K-Гo и первых (k — 1) способов необходимо выбрать Xk таким образом, чтобы выполнялись соотношения

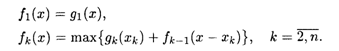
Рассмотрим конкретную задачу по распределению капита­ловложений между предприятиями.

< Предыдущая		Следующая >