27.2. Математическая модель нахождения компромиссного решения

Дана математическая модель экономической задачи, в ко­торой две целевые функции и система ограничений линейны. Найдем компромиссное решение по двум показателям, один из которых требует отыскания максимума, а другой — мини­мума:

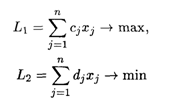
При ограничениях:

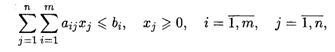
Где L1, L2 — значения целевых функций (экономические пока­затели), для упрощения записи опущены обозначения аргумен­та; Aij, Cj, Dj, Bi — коэффициенты; Xj — переменные.

Решим задачу по каждому показателю в отдельности и найдем оптимальные значения L1max, L2min.

Проделав преобразования над целевыми функциями, полу­чим математическую модель нахождения компромиссного ре­шения задачи с двумя целевыми функциями:

При ограничениях:

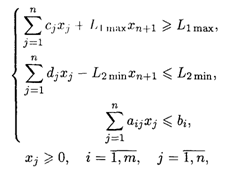
Где W — целевая функция; Xn+1 — наибольшее относительное значение экономических показателей.

Математическая модель будет аналогичной в случае на­хождения компромиссных решений задач, имеющих три целе­вые функции и более.

Рассмотрим нахождение компромиссного решения экономи­ческой задачи, математическая модель которой имеет три це­левые функции.

< Предыдущая		Следующая >