25.2. Линейное программирование с параметром в целевой функции

Пусть коэффициент Cj целевой функции изменяется в пре­делах (Cj — C'J,Cj + с''J), тогда для удобства решения задачи его можно заменить выражением

Где C'J, с''J — постоянные; λ — параметр, который изменяется в некоторых пределах (в общем случае от - до ).

В общем виде задача линейного программирования с пара­метром в целевой функции записывается так:

При ограничениях:

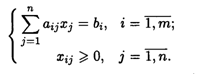
Для каждого значения λ в промежутке δ ≤ λ ≤ φ, где δ и φ — произвольные действительные числа, найти вектор (X1, X2,..., Xп), удовлетворяющий системе ограничений и об­ращающий в максимум (минимум) целевую функцию.

Решая задачу на максимум симплексным методом и иссле­дуя ее решение в зависимости от изменения параметра λ, полу­чим выражения для определения нижнего (λ1) и верхнего (λ2) его значений:

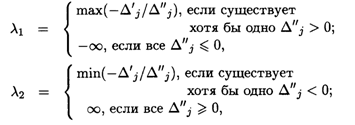
Где Δ"j, — оценка симплексной таблицы, содержащая пара­метр λ; Δ'J — оценка симплексной таблицы, не содержащая параметр λ.

Если для целевой функции отыскивается min, то границы изменения λ (λ1 и λ2) определяются следующим образом:

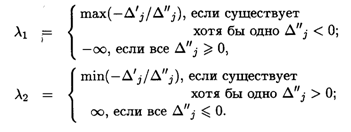
Приведем алгоритм решения.

1) Задачу решаем симплекс-методом при конкретном зна­чении параметра λ до получения оптимального решения.

2) Вычисляем значения параметров λ1, λ2.

3) Определяем множество значений параметра λ, для кото­рых полученное решение является оптимальным.

4) В случае необходимости в базис вводим вектор, соответ­ствующий столбцу, из которого определялось значение параметра λ2.

5) Выбираем ключевую строку и ключевой элемент.

6) Определяем новое оптимальное решение.

7) Находим новое множество значений λ, для которых ре­шение останется оптимальным.

8) Процесс вычисления повторяем до тех пор, пока весь от­резок [δ, φ] не будет исследован.

Выясним геометрический смысл задачи.

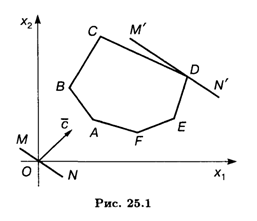
Пусть L() = (c'j + λC''jxj) → max. ABCDEF — область допустимых решений (рис. 25.1). При λ = 0 строим вектор и, перемещая линию уровня MN по направлению вектора , получим в точке D оптимальное решение. Итак, (D) — оп­тимальное решение, при котором имеем L( (D))Max. При различных значениях λ линия M'N', параллельная линии уров­ня MN, будет определенным образом поворачиваться вокруг точки D. Пусть при λ = λ1 прямая M'N' проходит через сторо­ну CD многоугольника допустимых решений, а при λ = λ2 — через сторону DE. Тогда значения (D)Опт и L((D))Max не изменятся до тех пор, пока λ1 ≤ λ ≤ λ2. Такая картина будет повторяться до получения нового оптимального решения, соот­ветствующего новой целевой функции, для которой существует свой диапазон изменения λ.

< Предыдущая		Следующая >