22.3. Решение двойственных задач. Решение симметричных задач
Рассмотрим решение задач с использованием теорем двойственности.

Решим исходную задачу графическим методом, получим ![]() Опт = (4, 1), при этом L(
Опт = (4, 1), при этом L(![]() )Mах = 3.
)Mах = 3.
На основании 1-й теоремы двойственности
![]()
Так как X1, Х2 > 0, то по 2-й теореме двойственности систему ограничений двойственной задачи можно записать в виде равенств:
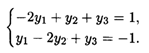
Подставим ![]() Опт в систему ограничений исходной задачи:
Опт в систему ограничений исходной задачи:
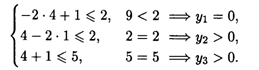
Тогда система ограничений двойственной задачи примет вид
![]()
Откуда ![]() Опт = (0, 2/3, 1/3), при этом S(
Опт = (0, 2/3, 1/3), при этом S(![]() )Min = 3.
)Min = 3.
Пусть дано решение двойственной задачи ![]() Опт = (0, 2/3, 1/3), S(
Опт = (0, 2/3, 1/3), S(![]() )Min = 3, найдем решение исходной.
)Min = 3, найдем решение исходной.
По 1-й теореме двойственности L(![]() )Max = S(
)Max = S(![]() )Min = 3. Так как У2, Y3 > 0, то по 2-й теореме двойственности второе и третье неравенства исходной задачи обращаются в равенства:
)Min = 3. Так как У2, Y3 > 0, то по 2-й теореме двойственности второе и третье неравенства исходной задачи обращаются в равенства:
![]()
Откуда ![]() Опт = (4,1), при этом L(
Опт = (4,1), при этом L(![]() )Mах = 3.
)Mах = 3.
Рассмотрим решение задач методом, основанным на взаимно однозначном соответствии между переменными: основным переменным исходной задачи соответствуют балансовые переменные двойственной, и наоборот. Для этого решим двойственную задачу симплексным методом:
![]()
При ограничениях:
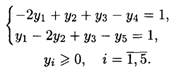
Из табл. 22.1 следует, что ![]() Опт = (0, 2/3, 1/3), S(
Опт = (0, 2/3, 1/3), S(![]() )Min = 3.
)Min = 3.

На основании 1-й теоремы двойственности получаем
![]()
Решение другой задачи найдем по соответствию между переменными:

Значение Xj определяем по последней симплексной таблице в строке ΔI в соответствующем столбце, причем значения Xj берем по модулю:
![]()
Таким образом, решение исходной задачи:
![]()
Если исходная задача решена симплексным методом, то решение двойственной задачи может быть найдено по формуле
![]()
Где С — матрица-строка коэффициентов при базисных переменных целевой функции в оптимальном решении исходной задачи; А-1 — обратная матрица для матрицы А, являющейся матрицей коэффициентов базисных переменных системы ограничений исходной задачи в оптимальном решении.
Решим симплексным методом исходную задачу вида
![]()
При ограничениях:
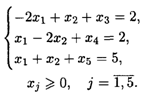
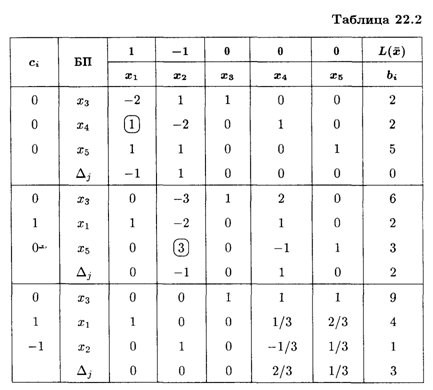
Из табл. 22.2 следует, что ![]() Опт = (4,1), L(
Опт = (4,1), L(![]() )max = 3. Матрицы записываются в виде
)max = 3. Матрицы записываются в виде
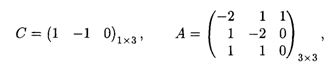
Тогда
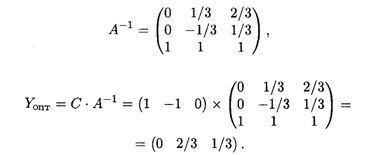
Таким образом, решение двойственной задачи следующее:
![]()
| < Предыдущая | Следующая > |
|---|