22.2. Основные теоремы двойственности

ТЕОРЕМА 1. Если одна из двойственных задач имеет оп­тимальное решение, то другая также имеет оптимальное решение, причем для любых оптимальных решений и вы­полняется равенство

Если одна из двойственных задач неразрешима ввиду то­го, что L()Max → (или S()Min → -), тo другая задача не имеет допустимых решений.

ТЕОРЕМА 2. Для оптимальности допустимых решений и пары двойственных задач необходимо и достаточно, что­бы они удовлетворяли системе уравнений

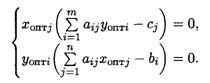
Теоремы позволяют определить оптимальное решение од­ной из пары задач по решению другой.

< Предыдущая		Следующая >