22.1. Двойственность в линейном программировании. Виды двойственных задач и составление их математических моделей. Симметричные двойственные задачи
Произвольную задачу линейного программирования можно определенным образом сопоставить с другой задачей линейного программирования, называемой Двойственной. Первоначальная задача является исходной. Эти две задачи тесно связаны между собой и образуют единую двойственную пару.
Различают симметричные, несимметричные и смешанные двойственные задачи.
Дана исходная задача
![]()
При ограничениях:
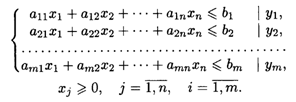
Задача дана в неканоническом виде. Составим математическую модель двойственной задачи, для этого:
— каждому неравенству системы ограничений исходной задачи приводим в соответствие переменную Yi;
— составляем целевую функцию, коэффициентами которой являются свободные члены системы ограничений исходной задачи;
— составляем систему ограничений. Коэффициенты системы ограничений образуют транспонированную матрицу коэффициентов системы ограничений исходной задачи. Знаки неравенств меняются на противоположные;
— свободными членами системы ограничений являются коэффициенты целевой функции исходной задачи. Все переменные двойственной задачи неотрицательные.
Математическая модель двойственной задачи имеет вид
![]()
При ограничениях:
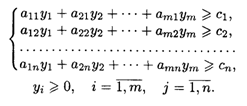
| < Предыдущая | Следующая > |
|---|