18.6.3. Эмпирическая функция распределения

Пусть Nх — число наблюдений, при которых значение при­знака Х меньше Х. При объеме выборки, равном П, относитель­ная частота события Х < х равна Nx/N.

Определение 8. Функция

Определяющая для каждого значения Х относительную частоту события Х < х, называется Эмпирической функцией распреде­ления, или функцией распределения выборки.

В отличие от эмпирической функции распределения F*(X) Выборки функция распределения F(X) генеральной совокупнос­ти называется Теоретической функцией распределения. Раз­личие между ними состоит в том, что функция F(X) опреде­ляет вероятность события Х < х, a F*(X) — относительную частоту этого события. Из теоретических результатов общей теории вероятностей (закон больших чисел) следует, что при больших П вероятность отличия этих функций друг от друга близка к единице:

Нетрудно видеть, что F*(X) обладает всеми свойствами F(X), что вытекает из ее определения (18.49):

1) значения F*(X) принадлежат отрезку [0, 1];

2) F*(X) является неубывающей функцией;

3) если Х1 — наименьшая варианта, то F*(X) = 0 при Х ≤ Х1; если Xk — максимальная варианта, то F*(X) = 1 при X > XK.

Сама же функция F*(X) служит для оценки теоретической функции распределения F(X) генеральной совокупности.

Пример 3. Построить эмпирическую функцию по заданному распределению выборки:

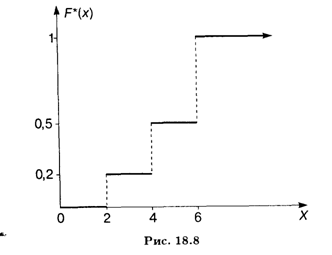
Решение. Находим объем выборки: П = 10 + 15 + 25 = 50. Наименьшая варианта равна 2, поэтому F*(X) = 0 при Х ≤ 2. Значение Х < 4 (или X1 = 2) наблюдалось 10 раз, значит, F*(X) = 10/50 = 0,2 при 2 < Х < 4. Значения X < 6 (а именно X1 = 2 и X2 = 4) наблюдались 10 + 15 = 25 раз, значит, при 4 < Х < 6 функция F*(X) = 25/50 = 0,5. Поскольку X = 6 — максимальная варианта, то F*(X) = 1 при Х > 6. Напишем формулу искомой эмпирической функции:

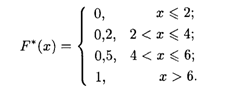
График этой функции показан на рис. 18.8.

< Предыдущая		Следующая >