18.5. Основные распределения непрерывных случайных величин. Равномерное распределение
Определение 1. Распределение вероятностей называется Равномерным, если на интервале возможных значений случайной величины плотность распределения является постоянной.
Пусть на интервале (A, B) плотность распределения является постоянной величиной: F(X) = С. Определим значение С из условия (18.35):
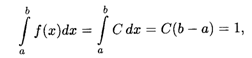
Откуда получаем, что F(X) = С = 1/(B - А). Значит, искомая плотность равномерного распределения дается формулой
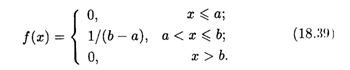
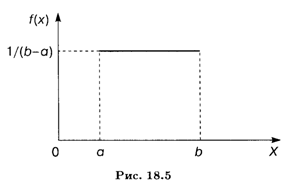
График плотности равномерного распределения указан на рис. 18.5.
Пример 1. Найти среднеквадратическое отклонение случайной величины X, распределенной равномерно на интервале (1, 5).
Решение. Согласно формуле (18.39), плотность распределения указанной случайной величины является ненулевой и равна 0,25 на интервале (1, 5). По формулам (18.36) и (18.38) последовательно вычисляем:
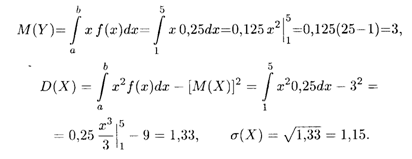
Пример 2. Радиус круга измерен приближенно на интервале (а, B). Полагая, что радиус является случайной величиной X, распределенной равномерно в этом интервале, найти математическое ожидание и дисперсию площади круга.
Решение. Площадь круга также является случайной величиной, вычисляемой по формуле Y = πX2; она имеет то же равномерное распределение, что и случайная величина X. По формулам (18.36) и (18.38) получаем
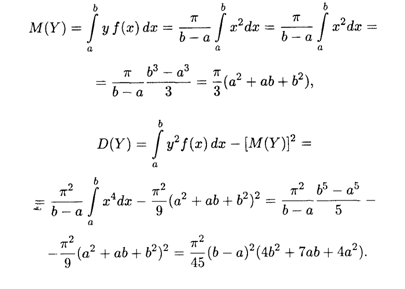
| < Предыдущая | Следующая > |
|---|