18.4.2. Числовые характеристики непрерывных случайных величин

Определения числовых характеристик дискретных случай­ных величин распространяются и на непрерывные величины. Разница состоит в том, что вместо сумм в формулах (18.5) и (18.10) берутся их интегральные аналоги.

Определение 4. Математическим ожиданием непрерывной случайной величины X, возможные значения которой находят­ся на отрезке [А, b], называется определенный интеграл:

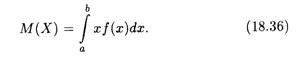
В том случае, когда возможные значения случайной вели­чины Х заполняют всю ось Ох, пределы интегрирования А и B бесконечны: А = -, B = . Возможны также случаи, ког­да один из пределов интегрирования бесконечен (возможные значения Х лежат на полупрямой).

Определение 5. Дисперсией непрерывной случайной величины Х называется математическое ожидание квадрата ее отклонения:

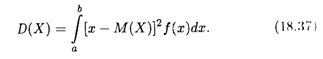
Все сказанное выше о случаях бесконечных пределов интегрирования остается справедливым и для дисперсии.

Среднее квадратичекое отклоенние непрерывной случайной величины определяется, как и прежде, по формуле (18.15):

σ(Х) = .

Для вычисления дисперсии употребляется более удобная фор­мула, которая выводится из (18.37):

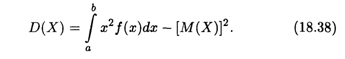
Пример 4. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X, Заданной плотностью распределения на отрезке [0, 1]:

Решение. Согласно формулам (18.36), (18.38) и (18.15) по­следовательно вычисляем искомые величины:

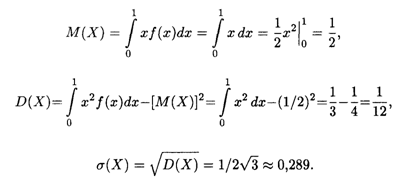
Пример 5. Найти основные числовые характеристики непре­рывной случайной величины X, заданной функцией распреде­ления на положительной полуоси Ох:

Решение. Найдем сначала плотность распределения:

Затем, как и в предыдущем примере, вычисляем соответствуцющие интегралы; при их вычислении применяем правило интегрирования по частям для определенного интеграла. В итоге получаем искомые величины:

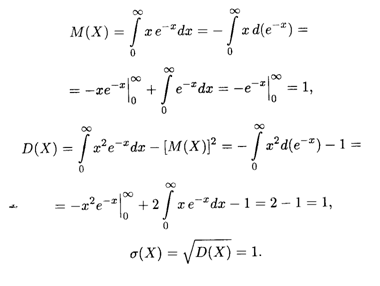
< Предыдущая		Следующая >