16.3.1. Линейная модель многоотраслевой экономики
В. В. Леонтьевым на основании анализа экономики США и период перед второй мировой войной был установлен важный факт: в течение длительного времени величины Aij = Xij / Xj Меняются очень слабо и могут рассматриваться как постоянные числа. Это явление становится понятным в свете того, что технология производства остается на одном и том же уровне довольно длительное время, и, следовательно, объем потребления J-Й отраслью продукции I-й отрасли при производстве своей продукции объема Xj есть технологическая константа.
В силу указанного факта можно сделать следующее допущение: для производства продукции J-Й отрасли объема Xj Нужно использовать продукцию I-й отрасли объема Aijxi, где Aij — постоянное число. При таком допущении технология производства принимается Линейной, а само это допущение называется Гипотезой линейности. При этом числа Аij называются Коэффициентами прямых затрат. Согласно гипотезе линейности, имеем
![]()
Тогда уравнения (16.2) можно переписать в виде системы уравнений
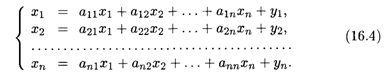
Введем в рассмотрение векторы-столбцы объемов произведенной продукции (вектор валового выпуска), объемов продукции конечного потребления (вектор конечного потребления) и матрицу коэффициентов прямых затрат:
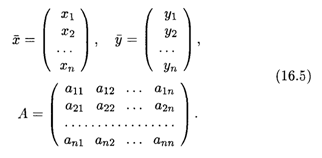
Тогда система уравнений (16.4) в матричной форме имеет вид
![]()
Обычно это соотношение называют Уравнением линейного межотраслевого баланса. Вместе с описанием матричного представления (16.5) это уравнение носит название Модели Леонтьева.
Уравнение межотраслевого баланса можно использовать в двух целях. В первом, наиболее простом случае, когда известен вектор валового выпуска ![]() , требуется рассчитать вектор конечного потребления
, требуется рассчитать вектор конечного потребления ![]() — подобная задача была рассмотрена выше (п. 16.1, пример 5).
— подобная задача была рассмотрена выше (п. 16.1, пример 5).
Во втором случае уравнение межотраслевого баланса используется для целей планирования со следующей формулировкой задачи: для периода времени T (например, год) известен вектор конечного потребления ![]() и требуется определить вектор
и требуется определить вектор ![]() валового выпуска. Здесь необходимо решать систему линейных уравнений (16.6) с известной матрицей А и заданным вектором
валового выпуска. Здесь необходимо решать систему линейных уравнений (16.6) с известной матрицей А и заданным вектором ![]() . В дальнейшем мы будем иметь дело именно с такой задачей.
. В дальнейшем мы будем иметь дело именно с такой задачей.
Между тем система (16.6) имеет ряд особенностей, вытекающих из прикладного характера данной задачи; прежде всего все элементы матрицы А и векторов ![]() и
и ![]() должны быть неотрицательными.
должны быть неотрицательными.
| < Предыдущая | Следующая > |
|---|