12.1.2. Скалярное произведение векторов

Определение 5. Скалярным произведением векторов (12.3) называется число, состоящее из суммы произведений соответ­ствующих координат этих векторов:

Как мы видим, формально такое определение скалярного произведения двух векторов согласуется с аналогичным опре­делением двух - и трехмерных векторов. Из данного определе­ния следуют основные свойства скалярного произведения век­торов:

1) = ;

2) (λ) = (λ) = λ(), где λ — действительное число;

3) (+) = + ;

4) > 0, если ≠ , и = 0, если = .

Введем понятие модуля вектора (его длины) и угла между векторами в виде обобщения на случай П > 3.

Определение 6. Для векторов из N-мерного векторного про­странства модуль вектора и угол φ между двумя ненулевыми векторами и определяются по формулам:

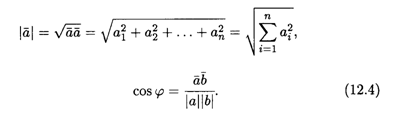
Укажем одно важное свойство векторов. Векторы и бу­дем называть Ортогональными, если их скалярное произведе­ние равно нулю:

Равенство (12.5) является аналогом условия перпендику­лярности векторов в двух - и трехмерном случаях, когда в ра­венстве (12.4) cosφ = 0.

< Предыдущая		Следующая >