08.5.4. Метод наименьших квадратов

Метод наименьших квадратов относится к методам Аппро­ксимации, или приближенного восстановления функции по из­вестным ее значениям в ряде точек. На практике часто возни­кает задача о наилучшем Подборе эмпирических формул, поз­воляющих представить в аналитической форме данные статис­тических наблюдений, измерений и т. д. Задача формулируется следующим образом: имеются данные наблюдений в П точках

Некоторой величины И и получены соответствующие значения

Нужно подобрать функцию определенного вида И = F(М), что­бы она по возможности наиболее точно отражала общую зави­симость измеряемой величины И от параметров (координат) точек измерения {МI}.

Таким образом, задача нахождения эмпирических формул состоит из двух этапов:

1) определение общего вида зависимости F(M) или вида функции F с точностью до постоянных параметров (коэффи­циентов), входящих в нее;

2) неизвестные коэффициенты подбираются таким образом, чтобы в точках наблюдений (8.14) подобранная функция как можно лучше отвечала данным измерений (8.15).

Итак, пусть на первом этапе определено, что эмпирическая формула должна включать совокупность известных базовых функций

Т. е. эта формула должна иметь вид

Где

— неизвестные параметры эмпирической функции.

Второй этап состоит в определении неизвестных парамет­ров (8.18). Их следует выбрать такими, чтобы значения функ­ции (8.17) по возможности наименее всего отклонялись в точ­ках (8.14) от измеренных значений (8.15).

Метод наименьших квадратов состоит в минимизации суммы квадратов Погрешностей (отклонений) δI (рис. 8.6) функции (8.17) в точках (8.14) как функции от Т аргумен­тов — неизвестных параметров:

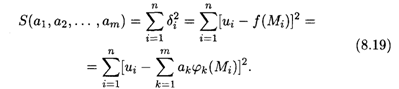
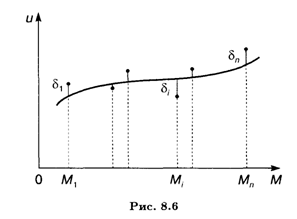
Для установления точки минимума функции (8.19) Т перемен­ных (8.18) нужно найти частные производные этой функции по всем Т аргументам и приравнять их к нулю. Отсюда полу­чается система Т линейных алгебраических уравнений отно­сительно Т неизвестных параметров (8.18)

Коэффициенты и свободные члены уравнений этой системы определяются по формулам

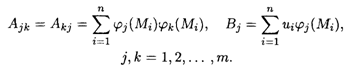
Поскольку функция (8.19) является положительной, выпуклой вниз и неограниченной в евклидовом пространстве Em, то ре­шение системы уравнений (8.20) представляет собой коорди­наты точки ее локального минимума.

При обработке данных экономической статистики наиболее распространенным является приближение эмпирической фор­мулой в виде линейной функции одной переменной (например, это широко используется в трендовом анализе). В этом случае совокупность точек измерения (8.14) представляет собой на­бор значений аргумента X1, Х2, ..., Xп, а совокупность функций (8.16) состоит из двух функций: X и 1. Эмпирическая формула (8.17) имеет вид

Неизвестные параметры А и B определяются из системы двух линейных уравнений

В которой коэффициенты и свободные члены выражаются фор­мулами

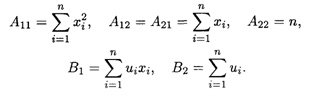
< Предыдущая		Следующая >