05.4.2. Максимизация прибыли

Пусть Q — количество реализованного товара, R(Q) — Функция дохода; C(Q) — функция затрат на производство то­вара. В реальности вид этих функций зависит в первую оче­редь от способа производства, организации инфраструктуры и т. п. Прибыль от реализации произведенного товара дается формулой

В микроэкономике известно утверждение: для того чтобы прибыль была максимальной, необходимо, чтобы предельный доход и предельные издержки были равны. Оба упомянутых предельных показателя определяются по аналогии с (5.14а), так что этот принцип можно записать в виде R'(Q) = C'(Q). Действительно, из необходимого условия экстремума для функ­ции (5.16) следует, что П'(Q) = 0, откуда и получается основ­ной принцип.

Пример 4. Найти максимум прибыли, если доход и издержки определяются следующими формулами:

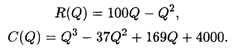
Решение. Согласно (5.16), прибыль П(Q) = - Q3 + 36Q2 - 69Q — 4000. Приравнивая производную функции прибыли к нулю, получаем уравнение

Корни этого уравнения Q1 = 1, Q2 = 23. Проверка показы­вает, что максимальная прибыль достигается при Q = 23: Пmах = 1290.

< Предыдущая		Следующая >