05.3.4. Схема исследования графика функции
Приведем схему исследования поведения функции и построения ее графика.
1. Найти область определения функции.
2. Определить возможный тип симметрии функции: четность или нечетность функции. Функция F(X) называется Четной, если выполнено условие симметрии ее графика относительно оси Оу:
![]()
Функция F(X) называется Нечетной, если выполнено условие симметрии ее графика относительно начала координат O (0, 0):
![]()
При наличии симметрии достаточно построить график функции на правой координатной полуплоскости и затем отобразить его на левую половину: зеркально относительно оси Оу в случае (5.10) (рис. 5.8,а) или с центральной симметрией в случае (5.11) (рис. 5.8,6).

3. Найти точки пересечения графика функции с осями координат Ох и Оу, т. е. решить соответственно уравнения У = F(0) и F(X) = 0.
4. Найти асимптоты.
5. Найти точки возможного экстремума.
6. Найти критические точки.
7. Исследовать знаки первой и второй производных, определить участки монотонности функции, направление выпуклости графика, точки экстремума и перегиба.
8. Определить максимум и минимум функции на области ее определения. Если областью определения функции является отрезок [А, b], необходимо вычислить значения функции в его концах и сопоставить их с локальными экстремумами.
9. Построить график функции с учетом проведенного исследования.
Пример 7. Исследовать и построить график функции

Решение. Действуем по приведенной выше схеме.
1. Область определения функции: Х ≠ 0 или Х ![]() (-
(-![]() , 0)
, 0) ![]() (0,
(0, ![]() ).
).
2. Функция (5.12) является нечетной, так как F(-X) = - F(X).
3. Уравнение F(X) = 0 дает корни Х = ±1 (точки пересечения с осью Ох). Пересечения с осью Оу нет в силу п.1.
4. Имеется вертикальная асимптота — ось Оу, так как предел F(X) при Х ![]() 0 бесконечен: F(X)
0 бесконечен: F(X) ![]() +
+![]() при Х
при Х ![]() 0-, F(X)
0-, F(X) ![]() -
-![]() при Х
при Х ![]() 0+.
0+.
Определяем наклонную асимптоту:
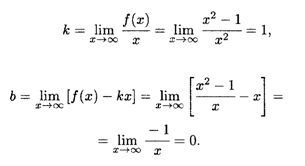
Итак, уравнение наклонной асимптоты: У = Х.
5. F'(X) = ![]() , т. е. производная нигде не равна нулю и точек возможного экстремума нет. В области определения везде F'(X) положительна.
, т. е. производная нигде не равна нулю и точек возможного экстремума нет. В области определения везде F'(X) положительна.
6. F"(X) = —2/х3 — критических точек нет.
7. Функция (5.12) монотонно возрастает на всей области своего определения, так как ее производная всюду положительна. В левой координатной полуплоскости выпуклость графика функции направлена вниз (F"(X) > 0), в правой полуплоскости выпуклость направлена вверх (F"(X) < 0).
8. Наибольшего и наименьшего значений функции не существует, поскольку область ее значений неограничена.
9. График функции (5.12) приведен на рис. 5.9.

| < Предыдущая | Следующая > |
|---|