05.3.3. Асимптоты графика функции

Часто оказывается, что график функции неограниченно приближается к некоторой прямой. Такого рода прямые назы­ваются Асимптотами. Неограниченность приближения графи­ка функции к асимптоте означает, что расстояние от графика до этой прямой (перпендикуляр, опущенный из произвольной точки графика на прямую) стремится к нулю.

Различают три вида асимптот: вертикальные, горизон­тальные и наклонные.

Определение 4. Прямая Х = а называется Вертикальной Асимптотой графика функции У = F(X), если хотя бы одно из предельных значений F(X) или F(X) равно + или -.

Вертикальные асимптоты обычно сопутствуют точкам раз­рыва второго рода. Например, график функции У = е1/x име­ет вертикальную асимптоту Х = 0, так как F(X) при Х 0+.

Определение 5. Прямая У = Kx + B называется наклонной асимптотой графика функции У = F(X) при Х ±, если F(X) Можно представить в виде

Где α(х) 0 при Х ±.

Это определение относится как к наклонной, так и к гори­зонтальной асимптотам: в случае горизонтальной асимптоты угловой коэффициент K в (5.9) равен нулю.

Укажем способ нахождения коэффициентов K и B в уравне­нии наклонной асимптоты. Разделив обе части равенства (5.9) на X и перейдя к пределу при Х , получим

Т. е. K = . Затем из равенства (5.9) находим:

Рассмотрим примеры: найти асимптоты графиков функ­ций.

Пример 5. F(X) = .

Решение. Найдем вертикальную асимптоту. Точка X = -1 является точкой разрыва 2-го рода, причем

Затем находим наклонные асимптоты:

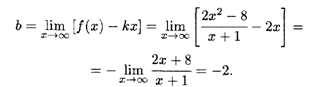
Таким образом, получаем уравнение наклонной асимптоты

Пример 6. F(X) = х + e-x.

Решение. Вертикальных асимптот здесь нет, поскольку точки разрыва 2-го рода отсутствуют. Отыщем наклонную асимптоту:

Таким образом, уравнение наклонной асимптоты имеет вид

< Предыдущая		Следующая >